Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta DFM\) vuông tại F có \(\angle FDM=45\Rightarrow\Delta DFM\) vuông cân tại F
\(\Rightarrow DF=FM\)
Vì \(\angle MFA=\angle MEA=\angle EAF=90\Rightarrow AEMF\) là hình chữ nhật
\(\Rightarrow AE=FM=DF\)
Xét \(\Delta DCF\) và \(\Delta ADE:\) Ta có: \(\left\{{}\begin{matrix}AD=CD\\DF=AE\\\angle DAE=\angle CDF=90\end{matrix}\right.\)
\(\Rightarrow\Delta DCF=\Delta ADE\left(c-g-c\right)\Rightarrow DE=CF\)
b) \(\Delta DCF=\Delta ADE\Rightarrow\angle DCF=\angle ADE\)
\(\Rightarrow\angle DCF+\angle DFC=\angle ADE+\angle DFC\Rightarrow\angle ADE+\angle DFC=90\)
\(\Rightarrow DE\bot FC\)
Tương tự chứng minh được: \(BF\bot CE\)
Gọi giao điểm của DE,BF là H \(\Rightarrow H\) là trực tâm tam giác CEF
\(\Rightarrow CH\bot EF\left(1\right)\)
FM cắt CB tại G,CM cắt AD tại I
Dễ dàng chứng minh được DCFG là hình chữ nhật
\(\Rightarrow CG=DF=AE\)
Ta có: \(MG=FG-FM=CD-FD==AD-FD=AF\)
Xét \(\Delta CMG\) và \(\Delta EFA:\) Ta có: \(\left\{{}\begin{matrix}MG=AF\\AE=CG\\\angle CGM=\angle EAF=90\end{matrix}\right.\)
\(\Rightarrow\Delta CMG=\Delta EFA\left(c-g-c\right)\Rightarrow\angle AFE=\angle CMG=\angle FMI\)
\(\Rightarrow\angle AFE+\angle FIM=\angle FMI+\angle FIM\Rightarrow\angle AFE+\angle FIM=90\)
\(\Rightarrow CM\bot EF\left(2\right)\)
Từ (1) và (2) \(\Rightarrow C,H,M\) thẳng hàng \(\Rightarrow\) đpcm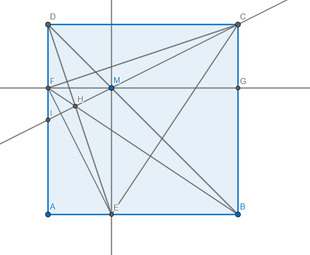


a) Chứng minh DE = CF, DE ⊥ CF
* Chứng minh DE = CF:
Ta có: \(\widehat{ABD}=45^o\) (BD là đường chéo của hình vuông)
=> \(\widehat{ABD}=\widehat{EMB}=45^o\) (Cùng phụ với \(\widehat{E}\))
=> ΔEMB cân tại E
Do đó: EM = EB
Mà: AEMF là hình chữ nhật (\(\widehat{A}=\widehat{E}=\widehat{F}\left(=90^o\right)\)
=> EM = FA
=> FD = AE (AD - FA = AB - ED)
Và: ΔvAED = ΔvDFC (2 cgv)
=> DE = CF
* Chứng minh DE ⊥ CF:
Ta có: \(\widehat{AED}+\widehat{ADE}=90^o\) (Trong tam giác có 1 góc vuông thì 2 góc còn lại tổng = 90o)
Mà: \(\widehat{AED}=\widehat{EDC}\) (so le trong)
\(\widehat{ADE}=\widehat{DCF}\) (ΔvAED = ΔvDFC)
=> \(\widehat{EDC}+\widehat{DCF}=90^o\)
=> DE ⊥ CF (Trong tam giác có tổng 2 góc = 90o thì góc còn lại là 1 góc vuông)
c) Xác định M để diện tích AEMF lớn nhất
Ta có: SAEMF = ME . MF
Và: ME + MF = AF + FD = AD
ME . MF lớn nhất <=> ME = MF
Do đó: AEMF là hình vuông
=> M là trung điểm của BD thì diện tích của AEMF lớn nhất

4:
Gọi giao của EF và CK là R
ER//DH
=>ER/DH=EK/DK
=>EB/DH+BR/DH=EK/DK
EB=AD
=>DA/DH=EK/DK-BR/DH(1)
BR//DH
=>SB/DS=BR/DH
=>BD/DS=BR/DH+1(2)
Từ (1), (2) suy ra \(\dfrac{DA}{DH}+\dfrac{DB}{DS}=\dfrac{EK}{DK}-\dfrac{BR}{DH}+\dfrac{BR}{DH}+1=\dfrac{DE}{DK}\)

A B C D E F
Xét tam giác vuông ABC, theo hệ thức lượng: \(BD=\frac{c^2}{a}.\)
Xét tam giác vuông BDA, ta có: \(m=EB=\frac{BD^2}{BA}=\frac{c^3}{a^2}\)
Hoàn toàn tương tự: \(n=\frac{b^3}{a^2}\)
Vậy thì \(a.m.n=\frac{b^3.c^3}{a^3}\)
Lại có: \(bc=ah\Rightarrow\frac{bc}{a}=h\Rightarrow\frac{b^3c^3}{a^3}=h^3\Rightarrow a.m.n=h^3.\)