Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E G H
a) \(\Delta ABC\) vuông tại A
\(\widehat{ABC+\widehat{ACB=90^o}}\)
\(55^o+\widehat{ACB=90^o}\)
\(\Rightarrow\widehat{ACB=35^o}\)
Nên \(\widehat{ACB< \widehat{ABC}}\)
\(\Rightarrow AB< AC\) (quan hệ giữa góc và cạnh đối diện trong tam giác).
b) Xét hai tam giác vuông ABD và AED có:
AB = AE (gt)
AD: cạnh chung
Vậy: \(\Delta ABD=\Delta AED\left(hcgv\right)\)
c) Hai trung tuyến BD và AF cắt nhau tại G nên G là trọng tâm của
\(\Delta ABC\)
Ta có: DG = \(\dfrac{1}{3}BD\)
Hai trung tuyến ED và AK cắt nhau tại H nên H là trọng tâm của
\(\Delta AEC\)
Ta có: DH = \(\dfrac{1}{3}ED\)
Mà BD = ED (\(\Delta ABD=\Delta AED\))
Nên DG = DH
Do đó: \(\Delta GDH\) cân tại D (đpcm).

a) Xét \(\Delta ABD\)và \(\Delta EBD\)có:
\(AB=EB\) (gt)
\(\widehat{ABD}=\widehat{EBD}\) (gt)
\(BD\) cạnh chung
suy ra: \(\Delta ABD=\Delta EBD\) (c.g.c)
b) \(\Delta ABD=\Delta EBD\) \(\Rightarrow\)\(AD=ED\)(2 cạnh tương ứng); \(\widehat{BAD}=\widehat{BED}=90^0\)(2 góc tương ứng)
Xét 2 tam giác vuông: \(\Delta DAM\)và \(\Delta DEC\)có:
\(DA=DE\) (cmt)
\(\widehat{ADM}=\widehat{EDC}\) (dd)
suy ra: \(\Delta DAM=\Delta DEC\) (cạnh góc vuông - góc nhọn kề cạnh ấy)
\(\Rightarrow\)\(AM=EC\)(2 cạnh tương ứng)
c) \(\Delta DAE\) cân tại D (do DA = DE)
\(\Rightarrow\)\(\widehat{DAE}=\widehat{DEA}\)
mà \(\widehat{DAM}=\widehat{DEC}\) ( \(=90^0\))
suy ra: \(\widehat{DAE}+\widehat{DAM}=\widehat{DEA}+\widehat{DEC}\)
hay \(\widehat{MAE}=\widehat{AEC}\) (đpcm)
a) Xét tam giác ABD và EBD có :
BA = BE;
Cạnh BD chung
\(\widehat{ABD}=\widehat{EBD}\)
\(\Rightarrow\Delta ABD=\Delta EBD\left(c-g-c\right)\)
b) Do \(\Delta ABD=\Delta EBD\Rightarrow AD=ED;\widehat{BAD}=\widehat{BED}=90^o\)
nên \(\widehat{DAM}=\widehat{DEC}\)
Vậy thì \(\Delta ABM=\Delta EDC\left(g-c-g\right)\)
\(\Rightarrow AM=EC\)
c) Ta có DA = DE nên \(\widehat{DAE}=\widehat{DEA}\)
Vậy nên \(\widehat{AEC}=\widehat{DEC}+\widehat{AED}=\widehat{DAM}+EAD=\widehat{EAM}\)

Xét ∆ABC và ∆DBC có:
AB = BD
Góc ABC = góc CBD
Góc BAC = góc BDC
=> ∆ABC = ∆DBC

Hình vẽ của mình chưa đúng nên bạn vẽ cho đúng nhé. còn cách làm thì đúng rồi đó.

a) Xét \(\Delta ABD\) và \(\Delta EBD\), ta có:
AB=EB (gt)
\(\widehat{ABD}=\widehat{EBD}\) ( vì BD là tia phân giác của \(\widehat{ABC}\))
BD chung
\(\Rightarrow\Delta ABD=\Delta EBD\) (c-g-c)
b) Vì \(\Delta ABD=\Delta EBD\)
\(\Rightarrow\) \(\widehat{BAD}=\widehat{BED}=90^0\) ( 2 góc tương ứng)
\(\Rightarrow AD=DE\) ( 2 cạnh tương ứng)
Ta có: \(\widehat{BAD}+\widehat{MAD}=180^0\)
\(90^0+\widehat{MAD}=180^0\)
\(\widehat{MAD}=90^0\)
Ta lại có: \(\widehat{BED}+\widehat{CED}=180^0\)
\(90^0+\widehat{CED}=180^0\)
\(\widehat{CED}=90^0\)
Xét \(\Delta MAD\) và \(\Delta CED\), ta có:
\(\widehat{CED}=\widehat{MAD}\) (cmt)
AD=DE ( cmt)
\(\widehat{ADM}=\widehat{EDC}\) ( đối đỉnh)
\(\Rightarrow\Delta MAD=\Delta CED\) (g-c-g)
\(\Rightarrow EC=AM\) ( 2 cạnh tương ứng)
c) Vì \(\Delta MAD=\Delta CED\)
\(\Rightarrow DC=DM\) ( 2 cạnh tướng ứng)
\(\Rightarrow\widehat{AMD}=\widehat{ECD}\) ( 2 góc tương ứng)
Ta có: MD+ DE=ME
DC+DA=AC
mà DC=DM, DE=DA nên ME=AC
Xét \(\Delta MAE\) và \(\Delta CEA\), ta có:
AM=EC (câu b)
\(\widehat{AMD}=\widehat{ECD}\) (cmt)
ME=AC (cmt)
\(\Rightarrow\Delta MAE=\Delta CEA\) ( c-g-c)
\(\Rightarrow\widehat{AEC}=\widehat{EAM}\) (2 góc tương ứng)

xét tan giác ABH và ACH
AB=AC (gt)
BH=BC (gt)
AH là cạnh chung
vây tam giác ABH=ACH (c.c.c)
vậy goc AHB=AHC (2 góc tương ứng)
vì AHB+AHC=180 (kề bù)
Mà AHB=AHC
vậy AHB=AHC=180:2=90
vậy AH vuông góc với BC
vi CB vuông góc Cx (gt)
AH vuông góc BC (cmt)
vậy Cx//AH
tam giác vuông EBC có E+B=90
tam giác vuông AHB có BAH+ B=90
Vậy BAH=BEC hay BAH=AEC

a, Tam giác ABC cân tại A nên \(\widehat{B}\) = \(\widehat{C}\)
⇒ \(\widehat{ABM}\) = \(\widehat{ACN}\) (1)
AB = AC (2)
\(\widehat{BAM}\) = \(\widehat{CAN}\) = 900 (3)
Kết hợp (1); (2) ; (3) ta có △BAM = △CAN (g-c-g)
b, BM = CN ( Δ BAM = ΔCAN)
BM = BN + MN = MN + MC
⇒ BN = CM
c, \(\widehat{BAN}\) + \(\widehat{NAC}\) = \(\widehat{BAC}\) =1200
\(\Rightarrow\) \(\widehat{BAN}\) = 1200 - \(\widehat{NAC}\) = 1200 - 900 = 300
\(\widehat{ABN}\) = (1800 - 1200) : 2 = 300
⇒ \(\widehat{BAN}\) = \(\widehat{ABN}\) = 300 ⇒ △ANB cân tại N

a) Xét hai tam giác BADBAD và BFDBFD có:
ABD^=FBD^ABD
=FBD
(vì BDBD là tia phan giác của góc BB);
AB=BFAB=BF (ΔABFΔABF cân tại BB);
BDBD là cạnh chung;
Vậy ΔBAD=ΔBFDΔBAD=ΔBFD (c.g.c).
b) ΔBAD =Δ BFDΔBAD =Δ BFD suy ra BAD^=BFD^=100∘BAD
=BFD
=100∘ (hai góc tương ứng).
Suy ra DFE^=180∘−BFD^=80∘DFE
=180∘−BFD
=80∘. (1)
Tam giác ABCABC cân tại AA nên B^=C^=180∘−100∘2=40∘B
=C
=2180∘−100∘=40∘
Suy ra DBE^=20∘DBE
=20∘.
Tương tự, tam giác BDEBDE cân tại BB nên BED^=180∘−20∘2=80∘BED
=2180∘−20∘=80∘. (2)
Từ (1) và (2) suy ra ΔDEFΔDEF cân tại DD.

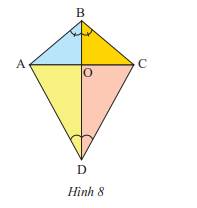
a) Tia BO là tia phân giác của \(\widehat {ABC}\) vì tia BO nằm giữa 2 tia BA và BC, tạo với 2 cạnh BA và BC 2 góc bằng nhau.
Tia DO là tia phân giác của \(\widehat {ADC}\) vì tia DO nằm giữa 2 tia DA và DC, tạo với 2 cạnh DA và DC 2 góc bằng nhau
b) Vì BO là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {ABO} = \widehat {CBO} = \frac{1}{2}.\widehat {ABC} = \frac{1}{2}.100^\circ = 50^\circ \)
Vì DO là tia phân giác của \(\widehat {ADC}\)nên \(\widehat {ADO} = \widehat {CDO} = \frac{1}{2}.\widehat {ADC} = \frac{1}{2}.60^\circ = 30^\circ \)
Vậy \(\widehat {ABO} = 50^\circ ;\widehat {ADO} = 30^\circ \)

a)
Xét 2 tam giác vuông ABD và tam giác ACE ta có
AB=AC ( do tam giác ABC là tam giác cân)
Góc A là góc chung
vậy tam giác ABD = tam giác ACE (ch-gn)
Ta có tam giác ABD =tam giác ACE ( chứng minh trên )
từ đó suy ra AD=AE
Nên suy ra tam giác AED là tam giác cân tại A
b)
gọi I là giao điểm của AH và ED
Xét 2 tam giác vuông AEH và tam giác ADH ta có
AE=AD ( chứng minh ở câu a)
góc D = gócE=90*
AH là cạnh chung
do đo tam giác AED = ADH ( c-g-c)
suy ra góc EAH=góc DAH ( do 2 góc tương ứng )
EH =HD ( do hai cạnh tương ứng )
suy ra H là trung điểm của ED (1)
Xét tam giác AEI và tam giác ADI ta có
AE=AD ( chứng minh câu a )
góc EAH=DAH (chứng minh trên )
AI là cạnh chung
Do đó tam giác AEI =tam giác ADI (c-g-c)
suy ra gócEIA= gócAID ( Do 2 góc tương ứng )
mà góc EIA +góc AID =180
Nên góc EIA=AID=90* (2)
tTừ (1) và ( 2) suy ra
AH là trung đểm của ED
CÒN CÂU C MÌNH LÀM SAU
c)
Ta có
AB=AC ( do tam giác ABC là tam giác cân tại A )
Mà AE=AD ( chứng minh câu a )
suy ra EB=DC
Xét 2 tam giác vuông tam giác EBC và tam giác DCB ta có
EB=DC ( chứng minh trên )
BC là cạnh chung
Do đó tam giác EBC=tam giác DCB ( ch-cgv)
suy ra EC=DB ( do hai cạnh tướng ứng )
Mà DK=DB
Suy ra EC=DK
Xét 2 tam giác vuông tam giác EBC và tam giác DCB ta có
EB=DC ( chứng minh trên )
Góc BEC =góc CDB =90*
EC=DK ( chứng minh trên )
do đó tam giác EBC =DCB ( C-G-C )
Suy ra góc ECB=góc DKC ( do hai góc tương ứng)
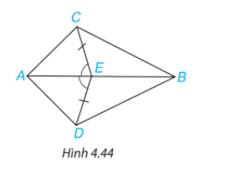


a)Xét hai tam giác AEC và AED có
\(EC = ED\)
\(\widehat {CEA} = \widehat {DEA}\)
AE chung
\( \Rightarrow \Delta AEC{\rm{ = }}\Delta AED\)(c.g.c)
b)
Do \(\Delta AEC{\rm{ = }}\Delta AED\) nên \(\widehat {CAE} = \widehat {DAE}\) ( 2 góc tương ứng) và AC=AD ( 2 cạnh tương ứng).
Xét \(\Delta ABC\) và \(\Delta ABD\) có:
AB chung
\(\widehat {CAE} = \widehat {DAE}\)
AC=AD
\( \Rightarrow \Delta ABC = \Delta ABD\)(c.g.c)