K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MB
1
NM
Cho hai tập hợp A = [ 1;3 ] và B = [ m; m+1], Tìm tất cả các giá trị của tham số m để \(B\subset A\)
1

3 tháng 11 2023
Để B là con của A
\(\left\{{}\begin{matrix}m\ge1\\m+1\le3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m\le2\end{matrix}\right.\)
Vậy 1 ≤ m ≤ 2

10 tháng 10 2023
\(A=\left[m;m+1\right]\)
\(B=\left[0;3\right]\)
\(A\cap B=\varnothing\)
\(\Leftrightarrow\left[{}\begin{matrix}m+1< 0\\m>3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>3\end{matrix}\right.\) thỏa mãn đề bài

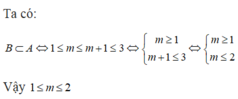


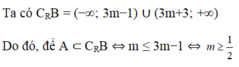
Lời giải:
Để \(B\subset A\) \(\left\{\begin{matrix} m+1\leq 1\\ m^2+2\geq 6\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\leq 0\\ m^2\geq 4\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m\leq 0\\ (m-2)(m+2)\geq 0\end{matrix}\right.\)
\(\Leftrightarrow m\leq -2\)