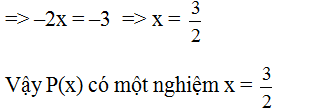Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho \(Q\left(x\right)=-x^{2016}+2015x-1=0\)
=> \(-x^{2016}=-\left(2015x-1\right)\)
=> \(x^{2016}=2015x-1\)
Nếu x có nghiệm âm thì \(x^{2016}\ge0\)và \(2015x-1< 0\)(không hợp lí)
Vậy x ko có nghiệm âm

a) \(P\left(x\right)=0\Rightarrow x^{2016}-x^{2014}=0\Rightarrow x^{2014}\left(x^2-1\right)=0\)
TH1: \(x^{2014}=0\Rightarrow x=0\)
TH2: \(x^2-1=0\Rightarrow x=\pm1\)
Vậy \(P\left(x\right)\) có nghiệm là \(x=0,x=1,x=-1\)
b) Xét \(x< 0\)
Ta có: \(x^{2016}>0\Rightarrow-x^{2016}< 0\); \(2015x< 0\)
\(\Rightarrow Q\left(x\right)=-x^{2016}+2015x-1< 0\)
Vậy \(Q\left(x\right)\) không có nghiệm âm
a, Đặt \(P\left(x\right)=x^{2016}-x^{2014}=0\Leftrightarrow x^{2014}\left(x^2-1\right)=0\Leftrightarrow x=0;x=-1;x=1\)

a) Nghiệm bằng 1 nha: 1^2016-1^2014=1-1=0
b)Không có nghiệm âm còn vì sao thì đợi lhi bạn k đug cho mk xog thì mk giải thick cho nha!
x2016-x2014=0
x2014*(x2-1)=0
TH1:
x2014=0
x=0
TH2
x2-1=0
x2=1
x=1
k mình nha

a) Ta có: P(x) = 0 khi 3 – 2x = 0
=>-2x = -3 => x = \(\dfrac{3}{2}\)
b) Q(x) =x2 +2 là đa thức không có nghiệm vì
x2 ≥ 0
2 > 0 (theo quy tắc nhân hai số hữu tỉ cùng dấu)
=>x2 + 2 > 0 với mọi x
Nên Q(x) không có nghiệm trong R
a) Ta có P(x) = 0 khi 3 – 2x = 0
b) Đa thức Q(x) không có nghiệm, bởi vì:
x2 ≥ 0 với mọi x thuộc R.
2 > 0
\(\Rightarrow\) Q(x) = x2 + 2 > 0 với mọi x thuộc R.
Do đó, không có giá trị x nào thuộc R để Q(x) = 0 hay đa thức Q(x) không có nghiệm.

\(a=\frac{6.2.3.4+6.3.4.5+6.4.5.6+...+6.98.99.100}{2.3.4+3.4.5+4.5.6+...+98.99.100}=6\)
thay vào p(x) suy ra a không là nghiệm của đa thức nhé bạn

Bài 1 :
\(A=x^2-2xy^2+y^4=\left(x-y^2\right)^2=-\left(y^2-x\right)^2\)
Mà \(B=-\left(y^2-x\right)^2\)
Nên ta có : đpcm
Bài 2
Đặt \(\left(x+1\right)\left(x-2\right)\left(2x-1\right)=0\)
TH1 : x = -1
TH2 : x = 2
TH3 : x = 1/2
Bài 4 :
a, \(\left(2x+3\right)\left(5-x\right)=0\Leftrightarrow x=-\frac{3}{2};5\)
b, \(\left(x-\frac{1}{2}\right)\left(3x+1\right)\left(2-x\right)=0\Leftrightarrow x=\frac{1}{2};-\frac{1}{3};2\)
c, \(x^2+2x=0\Leftrightarrow x\left(x+2\right)=0\Leftrightarrow x=0;-2\)
d, \(x^2-x=0\Leftrightarrow x\left(x-1\right)=0\Leftrightarrow x=0;1\)