Cho ba điểm A, B, C trên giây kẻ ô vuông (h.12). Hãy vẽ điểm thứ tư M sao cho A, B, C, M là bốn đỉnh của một hình bìn...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

SG

Sách Giáo Khoa

29 tháng 4 2017

Cho ba điểm A, B, C trên giây kẻ ô vuông (h.12). Hãy vẽ điểm thứ tư M sao cho A, B, C, M là bốn đỉnh của một hình bình hành ?

2

NT

Nguyen Thuy Hoa

29 tháng 6 2017

Hình bình hành

VK

Vu Kim Ngan

21 tháng 10 2018

Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG

Sách Giáo Khoa

21 tháng 4 2017

Đố :

Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32).

Hãy tìm điểm thứ tư M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình thang cân.

1

H

Hiiiii~

21 tháng 4 2017

Bài giải:

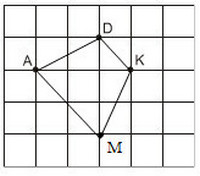
Có thể tìm được hai điểm M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho A, D, K là bốn đỉnh của một hình thang cân. Đó là hình thang AKDM₁ (với AK là đáy) và hình thang ADKM₂ (với DK là đáy).

DH

Đức Hiếu

8 tháng 9 2017

Có 5 hình cơ anh à =)

SG

Sách Giáo Khoa

29 tháng 4 2017

Các tứ giác ABCD, EFGH vẽ trên giấy kẻ ô vuông ở hình 7 có là hình bình hành không ?

1

NT

Nguyen Thuy Hoa

30 tháng 6 2017

Hình bình hành

PT

Pham Trong Bach

10 tháng 10 2019

Cho ba điểm A, B, C trên giấy kẻ ô vuông ở hình bên. Hãy vẽ điểm thứ tư M sao cho A, B,C, M là 4 đỉnh của một hình bình hành.

1

CM

Cao Minh Tâm

10 tháng 10 2019

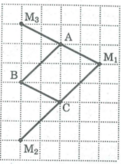
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

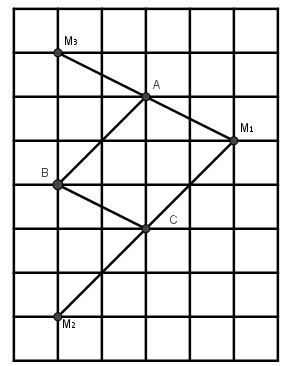
- Nếu hình bình hành nhận AC làm đường chéo vì AB là đường chéo hình vuông có 2 ô vuông nên C M 1 là đường chéo hình vuông cạnh 2 ô vuông và A, M 1 nằm trên một nửa mặt phẳng bờ BC ta có hình bình hành ABC M 1

- Nếu hình bình hành nhận BC làm đường chéo, điểm A cách điểm C ba ô vuông, điểm B cách điểm M 2 là ba ô vuông và trên một nửa mặt phẳng bờ AB ta có hình bình hành AB M 2 C

- Nếu hình bình hành nhận AB làm đường chéo thì điểm M 3 cách điểm B ba ô vuông, M 3 và A nằm trên cùng một nửa mặt phẳng bờ BC ta có hình bình hành ACB M 3

SG

Sách Giáo Khoa

21 tháng 4 2017

Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành không ?

1

HY

Hương Yangg

21 tháng 4 2017

Cả ba tứ giác là hình bình hành.

- Tứ giác ABCD là hình bình hành vì có

AB // CD và AB = CD =3 (dấu hiệu nhận biết 3)

- Tứ giác EFGH là hình bình hành vì có

EH // FG và EH = FH = 3 (dấu hiệu nhận biết 3)

- Tứ giác MNPQ là hình bình hành vì có MN = QP và MQ = NP (dấu hiệu nhận biết 2)

SG

Sách Giáo Khoa

21 tháng 4 2017

Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135)

Hãy chỉ ra :

a) Một điểm I sao cho \(S_{PIF}=S_{PAF}\)

b) Một điểm O sao cho \(S_{POF}=2.S_{PAF}\)

c) Một điểm N sao cho \(S_{PNF}=\dfrac{1}{2}S_{PAF}\)

1

TN

Tuyết Nhi Melody

21 tháng 4 2017

SG

Sách Giáo Khoa

21 tháng 4 2017

Cho hình 72, trong đó ABCD là hình bình hành

a) Chứng minh rằng AHCK là hình bình hành

b) Gọi O là trung điểm của HK. Chứng minh rằng 3 điểm A, O, C thẳng hàng

2

HY

Hương Yangg

21 tháng 4 2017

a) Hai tam giác vuông AHD và CKD có:

AD = CB (gt)

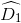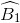= (so le trong)

Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)

Suy ra AH = CK

Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,

b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.

TM

Trần Minh Hoàng

29 tháng 9 2017

Tham khảo thôi!

a) Hai tam giác vuông AHD và CKD có:

AD = CB (gt)

\(\widehat{D_1}\) = \(\widehat{B_1}\) (so le trong)

Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)

Suy ra AH = CK

Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,

b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.

SG

Sách Giáo Khoa

29 tháng 4 2017

Cho hình 13 trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua điểm C

1

NT

Nguyen Thuy Hoa

30 tháng 6 2017

Đối xứng tâm

SG

Sách Giáo Khoa

29 tháng 4 2017

Hãy vẽ một số đa giác lồi mà các đỉnh là một số điểm trong các điểm đã cho ở hình dưới :

1

NT

Nguyen Thuy Hoa

1 tháng 7 2017

Đa giác. Đa giác đều

SG

Sách Giáo Khoa

6 tháng 5 2017

Hãy tính thể tích các hình dưới đây (h.143) theo các kích thước cho trên hình vẽ ?

1

NT

Nguyen Thuy Hoa

5 tháng 7 2017

Hình lăng trụ đứng. Hình chóp đều.

Hình lăng trụ đứng. Hình chóp đều.