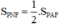Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
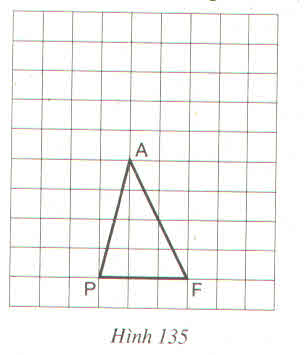
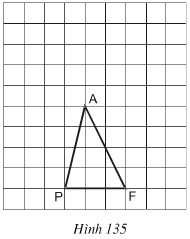
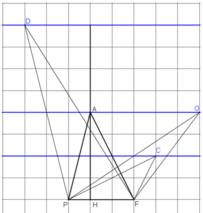
Gọi AH là chiều cao của tam giác APF.
Ta có: SAPF = AH.PF/2.
a) SPIF = SPAF
⇔ chiều cao IK = AH (Chung cạnh đáy PF).
⇔ I nằm trên đường thẳng song song với PF và cách PF 1 khoảng bằng AH.
b) SPOF = 2.SPAF
⇔ chiều cao OM = 2.AH
⇔ O nằm trên đường thẳng song song với PF và cách PF một khoảng bằng 2.AH
c)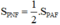 
⇔ chiều cao NQ = AH/2
⇔ N nằm trên đường thẳng song song với PF và cách PF một khoảng bằng AH/2.
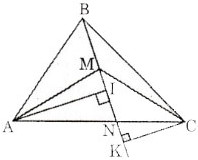
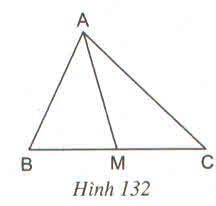
Theo giả thiết, M là điểm nằm trong tam giác ABC sao cho SMAC = SAMB + SBMC
Nhưng SAMB + SBMC + SMAC = SABC
Suy ra SMAC = SABC
∆ MAC = ∆ABC có chung đáy BC nên MK = 
BH. Vậy điểm M nằm trên đường trung bình EF của ∆ABC.
>>>>> Bí kíp học tốt các môn lớp 8 2017 bởi các Thầy C
Bai 1
Bo de : \(\Delta ABC\) trung tuyen AD
\(\Rightarrow S_{ADB}=S_{ADC}\)
cai nay ban tu chung minh nha
Ap dung bo de va bai nay => \(S_{MNPQ}=S_{MQP}+S_{MNP}=\frac{1}{3}S_{MDC}+\frac{1}{3}S_{ABP}\)
ta phai chung minh \(S_{MDC}+S_{ABP}=S_{ABCD}\)
That vay co \(S_{AMP}=S_{AMD},S_{MBP}=S_{MBC}\)
=> \(S_{ABP}+S_{MDC}=S_{ADM}+S_{MDC}+S_{MBC}=S_{ABCD}\)
=> dpcm
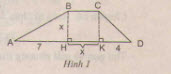
Hướng dẫn giải:
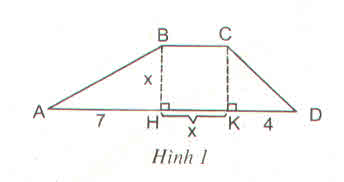
Gọi S là diện tích hình thang ABCD.
1) Theo công thức
S = BH(BC+DA)2BH(BC+DA)2
Ta có: AD = AH + HK + KD
=> AD = 7 + x + 4 = 11 + x
Do đó: S = x(11+2x)2x(11+2x)2
2) Ta có: S = SABH + SBCKH + SCKD.
= 1212.AH.BH + BH.HK + 1212CK.KD
= 1212.7x + x.x + 1212x.4
= 7272x + x2 + 2x
Vậy S = 20 ta có hai phương trình:
x(11+2x)2x(11+2x)2 = 20 (1)
7272x + x2 + 2x = 20 (2)
Cả hai phương trình không có phương trình nào là phương trình bậc nhất.
a) theo cách tính thứ nhất, diện tích hình thang là :
SABCD= BH.(BC+AD):2= x(x+7+x+4):2
=x(2x+11):2 = \(\dfrac{1}{2}\)x(2x+11) (đvdt) (1)
b) theo cách tính thứ hai
SABCD=SAHB+SCKD= \(\dfrac{1}{2}\).7x+x2+\(\dfrac{1}{2}\).4x
=\(\dfrac{7x+2x^2+4x}{2}\)= \(\dfrac{2x^2+11x}{2}\) (đvdt) (2)
Với S = 20 thì (1) và (2) trở thành x2+5,5x =20 thì đây là một phương trình bậc hai (vì có x2).
Vậy trong hai phương trình trên không có phương trình nào là phương trình bậc nhất.