Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
M B A H
kẻ MH vuông góc với AB.
Th1: H nằm trong đoạn AB (hình vẽ)
Đặt \(AB=c\).
áp dụng định lý pitago ta có: \(MA^2=MH^2+HA^2,MB^2=MH^2+HB^2\)
SUY RA: \(MA^2-MB^2=HA^2-HB^2=\left(HA-HB\right)\left(HA+HB\right)=a\)
Do H nằm trên đoạn AB nên HA+HB=a từ đó suy ra: \(HA-HB=\frac{a}{HA+HB}=\frac{a}{c}\)
Mà HA+HB=c suy ra: \(HA=\left(\frac{a}{c}+c\right):2=\frac{a+c^2}{2c}\)(không đổi).
Suy ra M nằm trên đường thẳng qua H ( H thuộc đoạn AB, \(HA=\frac{a+c^2}{2c}\)) vuông góc với AB.
TH2: H nằm ngoài đoạn AB ta có HA-HB=AB=c. Lập luận tương tự ta cũng có kết quả như TH1.
a) Vì = 90o (góc nội tiếp chắn nửa đường tròn) suy ra trong tam giác vuông MIB có tg
=
=
=>
= 26o34’
Vậy không đổi.
b) Phần thuận:
Khi điểm M chuyển động trên đường tròn đường kính AB thì điểm I cũng chuyển động, nhưng luôn nhìn đoạn thẳng AB cố định dưới góc 26o34’, vậy điểm I thuộc hai cung chứa góc 26o34’ dựng trên đoạn thẳng AB (hai cung 
và 
)
Phần đảo:
Lấy điểm I' bất kì thuộc hoặc , I'A cắt đường tròn đường kính AB tại M'.
Tam giác vuông BMT, có tg =
= tg26o34’
Kết luận: Quỹ tích điểm I là hai cung và
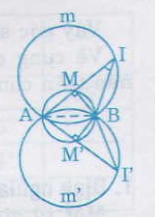
a) Vì \(\widehat{BMA}\)= 90o (góc nội tiếp chắn nửa đường tròn) suy ra trong tam giác vuông MIB có tg\(\widehat{AIB}\) = \(\dfrac{MB}{MI}\) = \(\dfrac{1}{2}\) =>\(\widehat{AIB}\) = 26o34’
Vậy \(\widehat{AIB}\) không đổi.
b) Phần thuận:
Khi điểm M chuyển động trên đường tròn đường kính AB thì điểm I cũng chuyển động, nhưng luôn nhìn đoạn thẳng AB cố định dưới góc 26o34’, vậy điểm I thuộc hai cung chứa góc 26o34’ dựng trên đoạn thẳng AB (hai cung và )
Phần đảo:
Lấy điểm I' bất kì thuộc hoặc , I'A cắt đường tròn đường kính AB tại M'.
Tam giác vuông BMT, có tg\(\widehat{I'}\) = \(\dfrac{M'B}{M'I'}\) = tg26o34’
Kết luận: Quỹ tích điểm I là hai cung và
Đây là bài toán về đường tròn Apollonius tỉ số k dựng trên đoạn AB. Ta giải như sau:
D A C B M I K
Trường hợp 1: k = 1. Khi đó ta thấy ngay MA = MB. Vậy quỹ tích những điểm M chính là đường trung trực của AB.
Trường hợp 2: \(k\ne1\).
Phần thuận. Gọi C, D là các điểm chia trong và chia ngoài đoạn thẳng AB theo tỉ số k. Ta có \(\frac{CA}{CB}=\frac{DA}{DB}=k\) (C nằm giữa A, B và D nằm ngoài đọan AB). Khi đó nếu M trùng C, D thì thỏa mãn đẳng thức.
Nếu M khác C và D. Ta có \(\frac{MA}{MB}=\frac{CA}{CB}=\frac{DA}{DB}\) nên MC, MD lần lượt là phân giác trong và phân giác ngoài của góc AMB. Do đó góc CMD = 90 độ hay M thuộc đường tròn đường kính CD.
Phần đảo. Lấy M bất kì thuộc đường tròn đường kính CD. Nếu M trùng C hoặc D thì xong.
Nếu M khác C và D. Qua A vẽ đuờng thẳng vuông góc với MC cắt MB tại I và cắt MC tại K. Ta có \(\frac{AI}{MD}=\frac{BA}{BD}=1-k\) . Vì \(k=\frac{DA}{DB}=\frac{CA}{CB}=\left(DC-2AC\right)\left(DB-BC\right)=1-\frac{2CA}{CD}\)nên \(\frac{AK}{MD}=\frac{AC}{CD}=\)\(\frac{1-k}{2}\) .Do đó AI = 2.AK, suy ra K là trung điểm AI, suy ra MI = MA. Từ đó \(\frac{MA}{MB}=\frac{MI}{MB}=\frac{DA}{DB}=k\). Vậy với k ≠ 1, quỹ tích những điểm M thỏa mãn \(\frac{MA}{MB}=k\) là đường tròn đường kính CD.
Chúc em học tốt :)