Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
C6. Cho các số thực dương thoả mãn: ab+1 nhỏ hơn hoặc bằng b Chứng minh rằng : ( a + (1/a^2) ) + ( b^2 + (1/b) ) lớn hơn hoặc bằng 9
\(ab+1\le b\Rightarrow a+\dfrac{1}{b}\le1\)
Đặt \(\left(a;\dfrac{1}{b}\right)=\left(x;y\right)\Rightarrow x+y\le1\)
Gọi vế trái của BĐT cần chứng minh là P:
\(P=x+\dfrac{1}{x^2}+y+\dfrac{1}{y^2}=\left(\dfrac{1}{x^2}+8x+8x\right)+\left(\dfrac{1}{y^2}+8y+8y\right)-15\left(x+y\right)\)
\(P\ge3\sqrt[3]{\dfrac{64x^2}{x^2}}+3\sqrt[3]{\dfrac{64y^2}{y^2}}-15.1=9\) (đpcm)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) hay \(\left(a;b\right)=\left(\dfrac{1}{2};2\right)\)
Áp dụng BĐT AM-GM ta có:
\(\left(a+1\right)^2+b^2+1=a^2+2a+1+b^2+1=\left(a^2+b^2\right)+2a+2\ge2\left(ab+a+1\right)\)
\(\Rightarrow\frac{1}{\left(a+1\right)^2+b^2+1}\le\frac{1}{2\left(ab+a+1\right)}\)(1)
\(\left(b+1\right)^2+c^2+1=b^2+2b+1+c^2+1=\left(b^2+c^2\right)+2b+2\ge2\left(bc+b+1\right)\)
\(\Rightarrow\frac{1}{\left(b+1\right)^2+c^2+1}\le\frac{1}{2\left(bc+b+1\right)}\)(2)
\(\left(c+1\right)^2+a^2+1=c^2+2c+1+a^2+1=\left(c^2+a^2\right)+2c+2\ge2\left(ca+c+1\right)\)
\(\Rightarrow\frac{1}{\left(c+1\right)^2+a^2+1}\le\frac{1}{2\left(ca+c+1\right)}\)(3)
Cộng vế theo vế của (1) ; (2) ; (3) ta được:
\(\frac{1}{\left(a+1\right)^2+b^2+1}+\frac{1}{\left(b+1\right)^2+c^2+1}+\frac{1}{\left(c+1\right)^2+a^2+1}\le\frac{1}{2}\left(\frac{1}{ab+a+1}+\frac{1}{bc+b+1}+\frac{1}{ca+c+1}\right)=\frac{1}{2}\)Dấu "=" xảy ra \(\Leftrightarrow a=b=b=1\)
Ta có: \(\frac{a}{1+b^2}=\frac{a\left(1+b^2\right)-ab^2}{1+b^2}=a-\frac{ab}{1+b^2}\)
\(1+b^2\ge2b\) \(\Rightarrow\frac{ab^2}{1+b^2}\le\frac{ab^2}{2b}=\frac{ab}{2}\)\(\Rightarrow-\frac{ab^2}{1+b^2}\ge-\frac{ab}{2}\)
Do đó: \(\frac{a}{1+b^2}=a-\frac{ab^2}{1+b^2}\ge a-\frac{ab}{2}\)
Tương tự: \(\frac{b}{1+c^2}\ge b-\frac{bc}{2}\); \(\frac{c}{1+a^2}\ge c-\frac{ca}{2}\)
Suy ra \(\frac{a}{1+b^2}+\frac{b}{1+c^2}+\frac{c}{1+a^2}+\frac{ab+bc+ca}{2}\ge a+b+c\)
Mặt khác ta có: \(3\ge\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{9}{a+b+c}\Rightarrow\frac{3}{a+b+c}\le1\)
\(\Rightarrow a+b+c\ge3\)
Do đó; \(\frac{a}{1+b^2}+\frac{b}{1+c^2}+\frac{c}{1+a^2}+\frac{ab+bc+ca}{2}\ge a+b+c\ge3\)(đpcm)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c=1\)
Ta có:
\(\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=\dfrac{1}{4a}+\dfrac{1}{4b}\)
Áp dụng bất đẳng thức AM-GM ta có:
\(\left\{{}\begin{matrix}\dfrac{1}{a+b}\le\dfrac{1}{2\sqrt{ab}}\\\dfrac{1}{4a}+\dfrac{1}{4b}\ge\dfrac{1}{2\sqrt{16ab}}=\dfrac{1}{2.4\sqrt{ab}}=\dfrac{1}{8\sqrt{ab}}\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{a+b}\le\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
Chúc bạn học tốt!!!
a) Giả sử ngược lại rằng a ≥ 1 và b ≥ 1. Ta suy ra a + b ≥ 2.
Điều này mâu thuẫn với giả thiết a + b < 2. Vậy một trong hai số a và b phải nhỏ hơn 1.
b) Giả sử ngược lại rằng n là số tự nhiên chẵn, n = 2k (k ∈ N). Khi đó 5n + 4 = 10k + 4 = 2(5k + 2) là một số chẵn. Điều này mâu thuẫn với 5n + 4 là số lẻ. Vậy nếu 5n + 4 là số lẻ thì n là số lẻ.
a) Giả sử ngược lại rằng a ≥ 1 và b ≥ 1. Ta suy ra a + b ≥ 2. Điều này mâu thuẫn với giả thiết a + b < 2.
Vậy một trong hai số a và b phải nhỏ hơn 1.
b) Giả sử ngược lại rằng n là số tự nhiên chẵn, n = 2k (k ∈ N). Khi đó 5n + 4 = 10k + 4 = 2(5k + 2) là một số chẵn. Điều này mâu thuẫn với 5n + 4 là số lẻ.
Vậy nếu 5n + 4 là số lẻ thì n là số lẻ.
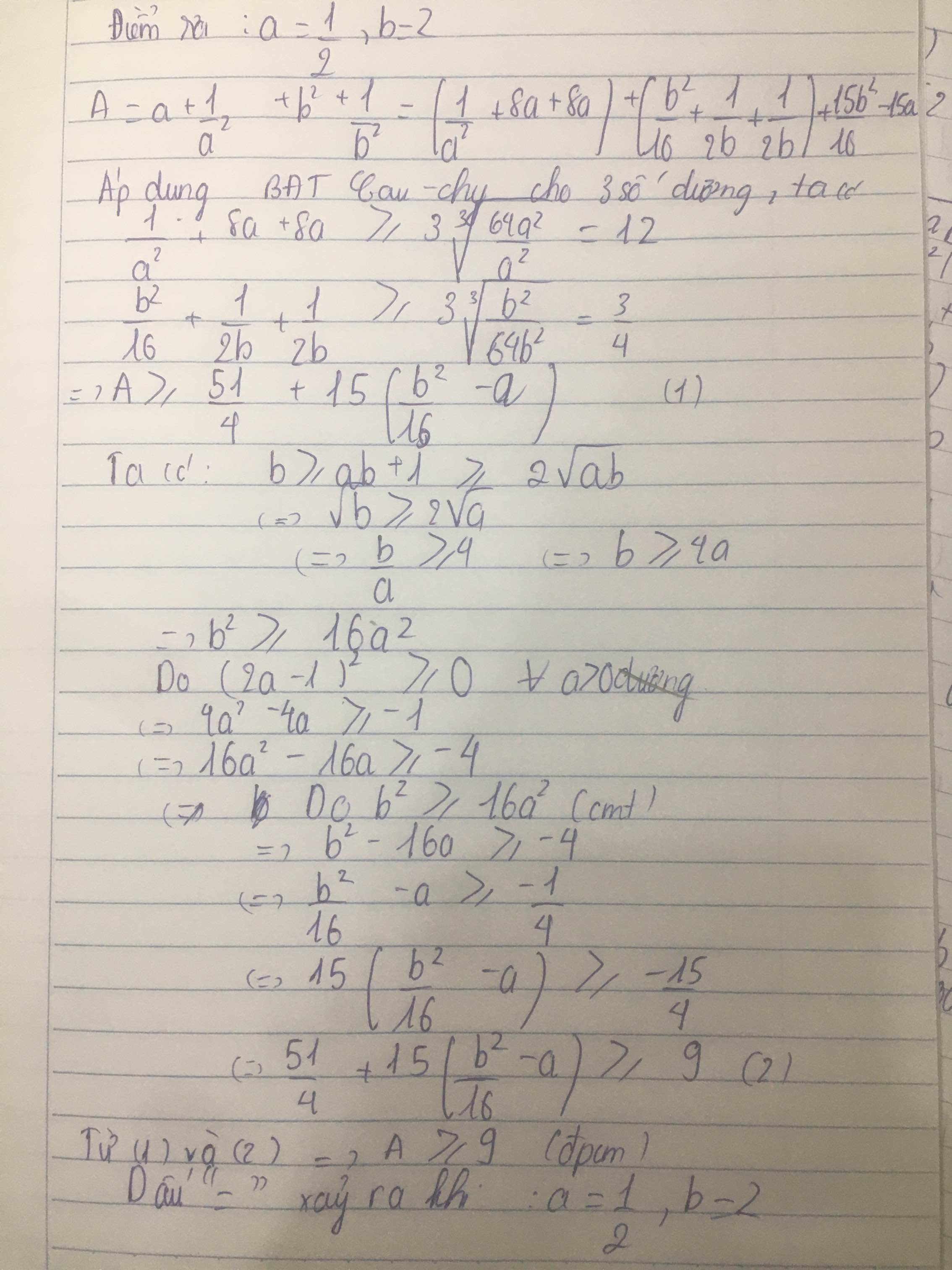
Với \(a,b>0\)
Ta có theo BĐT Cô-si:
\(a+b\ge2\sqrt{ab}\), và \(\frac{1}{a}+\frac{1}{b}\ge\frac{2}{\sqrt{ab}}\)
\(\Rightarrow\left(a+b\right)\left(\frac{1}{a}+\frac{1}{b}\right)\ge2\sqrt{ab}\cdot\frac{2}{\sqrt{ab}}=4\)
\(\Rightarrow\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\)
\(\Rightarrow\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}\right)\ge\frac{1}{a+b}\) hay \(\frac{1}{a+b}\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}\right)\)
(Dấu bằng xảy ra khi và chỉ khi \(a=b\))
Vậy \(\frac{1}{a+b}\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}\right)\) với \(a,b>0\).