Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là D
Gọi 4 số lập thành cấp số cộng là u1,u2,u3,u4 và công sai là d
Ta có: u2 = u1 + d; u3= u1 + 2d; u4 = u1 + 3d
Theo giả thiết ta có:
u
1
+
u
2
+
u
3
+
u
4
=
22
u
1
2
+
u
2
2
+
u
3
2
+
u
4
2
=
166
⇔
u
1
+
u
1
+
d
+
u
1
+
2
d
+
u
1
+
3
d
=
22
u
1
2
+
(
u
1
+
d
)
2
+
(
u
1
+
2
d
)
2
+
(
u
1
+
3
d
)
2
=
166
⇔
4
u
1
+
6
d
=
22
4
u
1
2
+
12
u
1
d
+
14
d
2
=
166
⇒
2
u
1
+
3
d
=
11
(
1
)
2
u
1
2
+
6
u
1
d
+
7
d
2
=
83
(
2
)
Từ (1) suy ra: u 1 = 11 − 3 d 2 thế vào (2) ta được:
2. 11 − 3 d 2 2 + 6. 11 − 3 d 2 . d + 7 d 2 = 83 ⇔ d = 3 ⇒ u 1 = 1 d = − 3 ⇒ u 1 = 10
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1
Tổng các lập phương của chúng:
1 3 + 4 3 + 7 3 + 10 3 = 1408

Lời giải:
Gọi số hạng đầu tiên là $a$ và công sai $d$. Khi đó số hạng thứ 2 và 3 lần lượt là $a+d, a+2d$
Theo bài ra ta có:
$a+(a+d)+(a+2d)=12$
$\Rightarrow a+d=4$
$a^2+(a+d)^2+(a+2d)^2=66$
$\Leftrightarrow 3a^2+5d^2+6ad=66$
$\Leftrightarrow 3(4-d)^2+5d^2+6(4-d)d=66$
$\Leftrightarrow 2d^2-18=0$
$\Leftrightarrow d=\pm 3$
Nếu $d=3$ thì $a=1$. Khi đó 3 số cần tìm là $1,4, 7$
Nếu $d=-3$ thì $a=7$. Khi đó 3 số cần tìm là $7, 4, 1$
\(S_3=\dfrac{3\left[2u_1+2d\right]}{2}\)
\(\Leftrightarrow2u_1+2d=\dfrac{2S_3}{3}\)
\(\Leftrightarrow2\left(u_1+d\right)=\dfrac{2S_3}{3}\)
\(\Leftrightarrow u_1+d=\dfrac{S_3}{3}=\dfrac{12}{3}=4\)
\(\Rightarrow\left\{{}\begin{matrix}u_1=1\\d=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_2=4\\u_3=7\end{matrix}\right.\)
mà \(u_1^2+u_2^2+u_3^2=1^2+4^2+7^2=66\) (thỏa đề bài)
Vậy 3 số hạng liên tiếp của 1 cấp số cộng là : \(1;4;7\)

Chọn A
Giả sử bốn số hạng đó là a − 3 x ; a − x ; a + x ; a + 3 x với công sai là d =2x. Khi đó, ta có:
a − 3 x + a − x + a + x + a + 3 x = 20 a − 3 x 2 + a − x 2 + a + x 2 + a + 3 x 2 = 120
⇔ 4 a = 20 4 a 2 + 20 x 2 = 120 ⇔ a = 5 x = ± 1
Vậy bốn số cần tìm là 2; 4; 6; 8.
Tổng của 2 số hạng đầu tiên là: 2+ 4= 6.

Đáp án C
Gọi d = 2 x là công sai
ta có bốn số là a - 3 x , a - x , a + x , a + 3 x
Khi đó, từ giả thiết ta có:
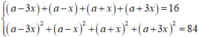
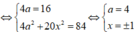
⇔ 1 , 3 , 5 , 7 7 , 5 , 3 , 1
Tổng bình phương của số hạng đầu và cuối là 1 2 + 7 2 = 50

Gọi công sai của cấp số cộng là d; số hạng đầu là u1 = x - d, u2 = x, u3 = x + d.
CSC tăng nên d > 0.
Theo giả thiết, ta có hệ:
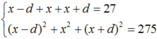
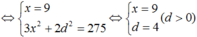
Vậy cấp số cộng cần tìm là : 5, 9, 13 .

Gọi d là công sai. Ba số phải tìm là \(\left(x-d\right);x;\left(x+d\right)\), ta có hệ phương trình :
\(\begin{cases}\left(x-d\right)+x+\left(x+d\right)=9\left(1\right)\\\left(x-d\right)^2+x^2+\left(x+d\right)^2=125\left(2\right)\end{cases}\)
(1) \(\Leftrightarrow3x=9\Rightarrow x=3\)
(2)\(\Leftrightarrow\left(3-d\right)^2+3^2+\left(3+d\right)^2=125\Leftrightarrow d=\pm7\)
Với d = 7 cấp số là : -4 ; 3 ; 10
Với d = -7 cấp số là 10; 3 ; -4
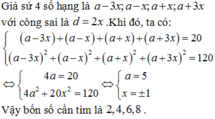
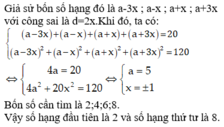
Gọi 4 số lập thành cấp số cộng là u1,u2,u3,u4
Ta có:
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1
Tổng các lập phương của chúng: 13+43+73+ 103=1408
Đáp án là D