K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

KV
5 tháng 10 2023
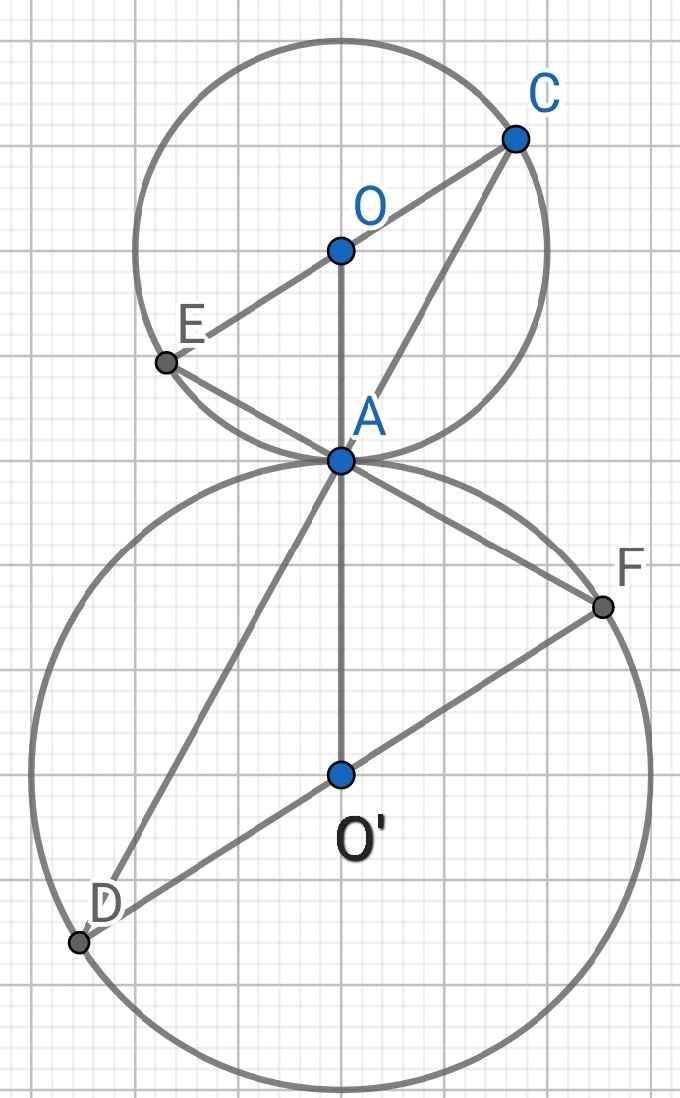
a) Đặt R là bán kính đường tròn tâm O
r là bán kính đường tròn tâm O'
Ta có:
OC = OA = R
⇒ ∆OAC cân tại O
⇒ ∠OAC = ∠OCA
Mà ∠OAC = ∠O'AD (đối đỉnh)
⇒ ∠OCA = ∠O'AD (1)
Lại có:
O'A = OD = r
⇒ ∆O'AD cân tại O'
⇒ ∠O'AD = ∠O'DA (2)
Từ (1) và (2) suy ra ∠OCA = ∠O'DA
b) Do ∠OCA = ∠O'DA (cmt)
Mà ∠OCA và ∠O'DA là hai góc so le trong
⇒ OC // O'D
c) Do CE là đường kính của đường tròn tâm O
A nằm trên đường tròn tâm O
⇒ ∆ACE vuông tại A
Hay AC ⊥ AE
d) Do DF là đường kính của đường tròn tâm O'
A nằm trên đường tròn tâm O'
⇒ ∆DAF vuông tại A
⇒ AD ⊥ AF⇒ AC ⊥ AF
Lại có AC ⊥ AE
⇒ E, A, F thẳng hàng
⇒ ∠OAE = ∠O'AF (đối đỉnh)
a) Đặt R là bán kính đường tròn tâm O
r là bán kính đường tròn tâm O'
Ta có:
OC = OA = R
∆OAC cân tại O
⇒ ∠OAC = ∠OCA
Mà ∠OAC = ∠O'AD (đối đỉnh)
⇒ ∠OCA = ∠O'AD (1)
Lại có:
O'A = OD = r
⇒ ∆O'AD cân tại O'
⇒ ∠O'AD = ∠O'DA (2)
Từ (1) và (2) suy ra ∠OCA = ∠O'DA
b) Sửa đề: chứng minh OC // O'D
Do ∠OCA = ∠O'DA (cmt)
Mà ∠OCA và ∠O'DA là hai góc so le trong
⇒ OC // O'D
c) Do CE là đường kính của đường tròn tâm O
A nằm trên đường tròn tâm O
⇒ ∆ACE vuông tại A
Hay AC ⊥ AE