Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

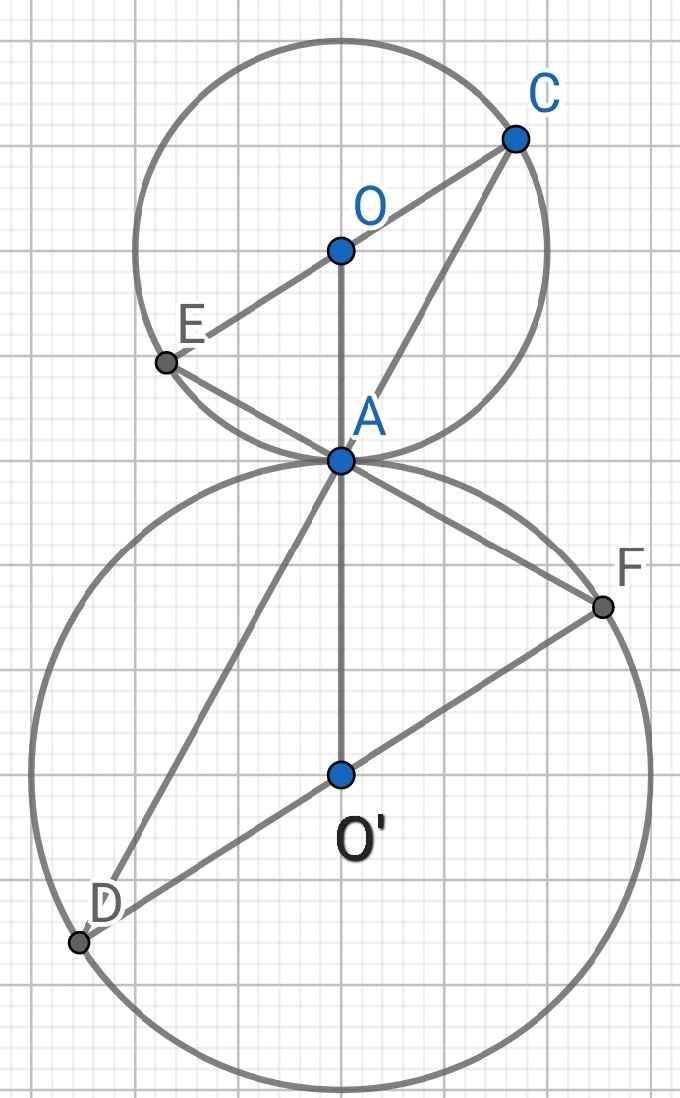
a) Đặt R là bán kính đường tròn tâm O
r là bán kính đường tròn tâm O'
Ta có:
OC = OA = R
∆OAC cân tại O
⇒ ∠OAC = ∠OCA
Mà ∠OAC = ∠O'AD (đối đỉnh)
⇒ ∠OCA = ∠O'AD (1)
Lại có:
O'A = OD = r
⇒ ∆O'AD cân tại O'
⇒ ∠O'AD = ∠O'DA (2)
Từ (1) và (2) suy ra ∠OCA = ∠O'DA
b) Sửa đề: chứng minh OC // O'D
Do ∠OCA = ∠O'DA (cmt)
Mà ∠OCA và ∠O'DA là hai góc so le trong
⇒ OC // O'D
c) Do CE là đường kính của đường tròn tâm O
A nằm trên đường tròn tâm O
⇒ ∆ACE vuông tại A
Hay AC ⊥ AE

Bài 2:
a: Xét (O) có
CM,CA là tiếp tuyến
nên OC là phân giác của góc MOA(1) và CM=CA
Xet (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
b:
Xét ΔCOD vuông tại O có OM là đường cao
nên MC*MD=OM^2
c: \(AC=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
a) Đặt R là bán kính đường tròn tâm O
r là bán kính đường tròn tâm O'
Ta có:
OC = OA = R
⇒ ∆OAC cân tại O
⇒ ∠OAC = ∠OCA
Mà ∠OAC = ∠O'AD (đối đỉnh)
⇒ ∠OCA = ∠O'AD (1)
Lại có:
O'A = OD = r
⇒ ∆O'AD cân tại O'
⇒ ∠O'AD = ∠O'DA (2)
Từ (1) và (2) suy ra ∠OCA = ∠O'DA
b) Do ∠OCA = ∠O'DA (cmt)
Mà ∠OCA và ∠O'DA là hai góc so le trong
⇒ OC // O'D
c) Do CE là đường kính của đường tròn tâm O
A nằm trên đường tròn tâm O
⇒ ∆ACE vuông tại A
Hay AC ⊥ AE
d) Do DF là đường kính của đường tròn tâm O'
A nằm trên đường tròn tâm O'
⇒ ∆DAF vuông tại A
⇒ AD ⊥ AF⇒ AC ⊥ AF
Lại có AC ⊥ AE
⇒ E, A, F thẳng hàng
⇒ ∠OAE = ∠O'AF (đối đỉnh)