Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a,Ta có \(\dfrac{1}{2.3}\)=\(\dfrac{1}{6}\)
\(\dfrac{1}{2}-\dfrac{1}{3}\)=\(\dfrac{3}{6}-\dfrac{2}{6}\)=\(\dfrac{1}{6}\)
=>\(\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)
b, \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2005.2006}\)
=\(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+....+\dfrac{1}{2005}-\dfrac{1}{2006}\)
=\(\dfrac{1}{1}-\dfrac{1}{2006}\)
=\(\dfrac{2006}{2006}-\dfrac{1}{2006}\)
=\(\dfrac{2005}{2006}\)
Ta có
\(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{\left(n+1\right)-n}{n.\left(n+1\right)}=\dfrac{1}{n.\left(n+1\right)}\)
Vậy \(\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)
a.
\(\frac{1}{2\times3}=\frac{1}{6}\)
\(\frac{1}{2}-\frac{1}{3}=\frac{3}{6}-\frac{2}{6}=\frac{1}{6}\)
\(\Rightarrow\frac{1}{2\times3}=\frac{1}{2}-\frac{1}{3}\)
b.
\(\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+.....+\frac{1}{2005\times2006}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+.....+\frac{1}{2005}-\frac{1}{2006}\)
\(=1-\frac{1}{2006}\)
\(=\frac{2005}{2006}\)
Chúc bạn học tốt
(n ∈ N) là phân số tối giản.
có giá trị là số nguyên.
Gọi d là ƯCLN(2n+5,n+3)(d\(\in\)N*)
Ta có:\(2n+5⋮d,n+3⋮d\)
\(\Rightarrow2n+5⋮d,2\cdot\left(n+3\right)⋮d\)
\(\Rightarrow2n+5⋮d,2n+6⋮d\)
\(\Rightarrow\left(2n+6\right)-\left(2n+5\right)⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
Vì ƯCLN(2n+5,n+3)=1
\(\Rightarrow\frac{2n+5}{n+3}\) là phân số tối giản
Gọi d là ƯCLN(2n+5,n+3)(d∈
N*)
Ta có:2n+5⋮d,n+3⋮d
⇒2n+5⋮d,2⋅(n+3)⋮d
⇒2n+5⋮d,2n+6⋮d
⇒(2n+6)−(2n+5)⋮d
⇒1⋮d⇒d=1
Vì ƯCLN(2n+5,n+3)=1
Bài 3.
Tính số học sinh của lớp 6A.
lớp của 6A trường câụ là bao nhiêu rồi ghi vó là được
chúc bạn học tốt
6 và b
Câu 3 : A
Câu 4 : B
Câu 5 : A
Câu 8 :
a) 7x - 8 = 713
7x = 713 + 8
7x = 721
x = 721 : 7
x = 103
b) 2448 : [ 119 - ( x- 6 ) ] = 24
119 - ( x - 6 ) = 2448 : 24
119 - ( x - 6 ) = 102
x - 6 = 119 - 102
x - 6 = 17
x = 17 + 6
x = 23
c) 2016 - 100 . ( x + 11 ) = 27 : 23
2016 - 100 . ( x + 11 ) = 24
2016 - 100 . ( x + 11 ) = 16
100 . ( x + 11 ) = 2016 - 16
100 . ( x + 11 ) = 2000
x + 11 = 2000 : 100
x + 11 = 20
x = 20 - 11
x = 9
Câu 9 : tự làm nhé , bài này dễ rồi
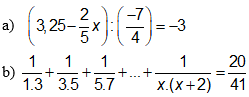
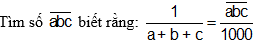
Câu 11 :
b) Tính \(\dfrac{1}{1.2} + \dfrac{1}{2.3} + \dfrac{1}{3.4} + ... + \dfrac{1}{2005.2006}\)
= \(\dfrac{1}{1} - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} +...+ \dfrac{1}{2005} - \dfrac{1}{2006}\)
= \(1 - \dfrac{1}{2006}\)
= \(\dfrac{2005}{2006}\)