
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4x^2 - 7x -2 = 4x^2 - 8x + x - 2 = 4x(x - 2) + (x - 2) = (x -2)(4x + 1)

a) \(\sqrt{\left(\sqrt{2}-1\right)^2}-\sqrt{11+6\sqrt{2}}\)
\(=\sqrt{2}-1-3-\sqrt{2}\)
=-4
b) \(\sqrt{\left(1-\sqrt{5}\right)^2}+\sqrt{14-6\sqrt{5}}\)
\(=\sqrt{5}-1+3-\sqrt{5}\)
=2
c) \(\sqrt{21-12\sqrt{3}}-\sqrt{13-4\sqrt{3}}\)
\(=2\sqrt{3}-3-2\sqrt{3}+1\)
=-2

Ta có: (căn x+y)2=(căn x+z + căn y+x)2
suy ra:x+y=(căn x+z)2 +2(căn x+z)(căn y+z)+(căn y+z)2
suy ra:x+y=x+z+y+z+2[căn (x+z)(y+z)]
suy ra:-z=căn (x+z)(y+z)
suy ra:(-z)2=[căn (x+z)(y+z)]2
suy ra:z2=(x+z)(y+z)
suy ra:z2=xy+xz+yz+z2
suy ra:xy+yz+xz=0
suy ra:(xy+yz+xz)/xyz=0(vì x,y,z khác 0)
suy ra:xy/xyz+yz/xyz+xz/xyz=0
suy ra:1/x+1/y+1/z=0(ĐPCM)
K CHO MÌNH VỚI NHA

a) \(17-12\sqrt{2}=\left(3-2\sqrt{2}\right)^2\)
b) \(57-24\sqrt{3}=\left(4\sqrt{3}-3\right)^2\)
c) \(x+2\sqrt{2x-4}=\left(\sqrt{x-2}+\sqrt{2}\right)^2\)

\(\sqrt{a}+\sqrt{b}\ge\sqrt{a+b}\)
Bình 2 vế của pt do 2 vế dương ta có:
\(\left(\sqrt{a}+\sqrt{b}\right)^2\ge\left(\sqrt{a+b}\right)^2\)
\(\Leftrightarrow a+b+2\sqrt{ab}\ge a+b\)
\(\Leftrightarrow2\sqrt{ab}\ge0\Leftrightarrow\sqrt{ab}\ge0\) (luôn đúng)
Tức ta có điều phải cm

\(\sqrt{21-12\sqrt{3}}=\sqrt{21-2.\sqrt{36}.\sqrt{3}}=\sqrt{21-2\sqrt{108}}=\sqrt{12-2.\sqrt{12}.\sqrt{9}+9}=\sqrt{\left(\sqrt{12}-3\right)^2}=\sqrt{12}-3\)

a, \(2\sqrt{3}-\sqrt{4+x^2}=0\Leftrightarrow\sqrt{4+x^2}=2\sqrt{3}\)
\(\Leftrightarrow x^2+4=12\Leftrightarrow x^2=8\Leftrightarrow x=\pm2\sqrt{2}\)
b, \(\sqrt{16x+16}-\sqrt{9x+9}=0\)ĐK : x >= -1
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=0\Leftrightarrow\sqrt{x+1}=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
c, \(\sqrt{4\left(x+2\right)^2}=8\Leftrightarrow2\left|x+2\right|=8\Leftrightarrow\left|x+2\right|=4\)
TH1 : \(x+2=4\Leftrightarrow x=2\)
TH2 : \(x+2=-4\Leftrightarrow x=-6\)
c: Ta có: \(\sqrt{4\left(x+2\right)^2}=8\)
\(\Leftrightarrow\left|x+2\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=4\\x+2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)
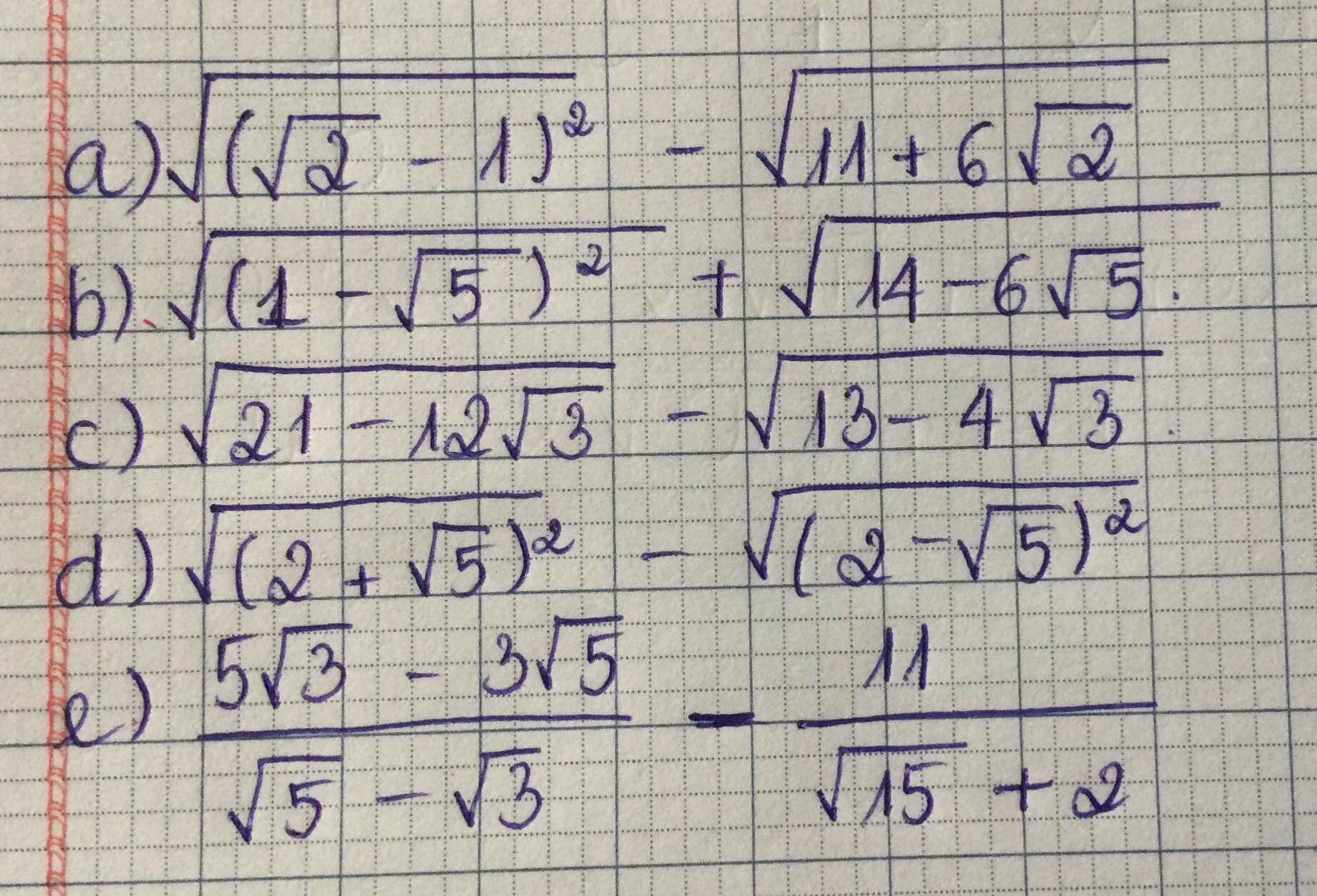 Tính và thu gọn biểu thức.
Tính và thu gọn biểu thức.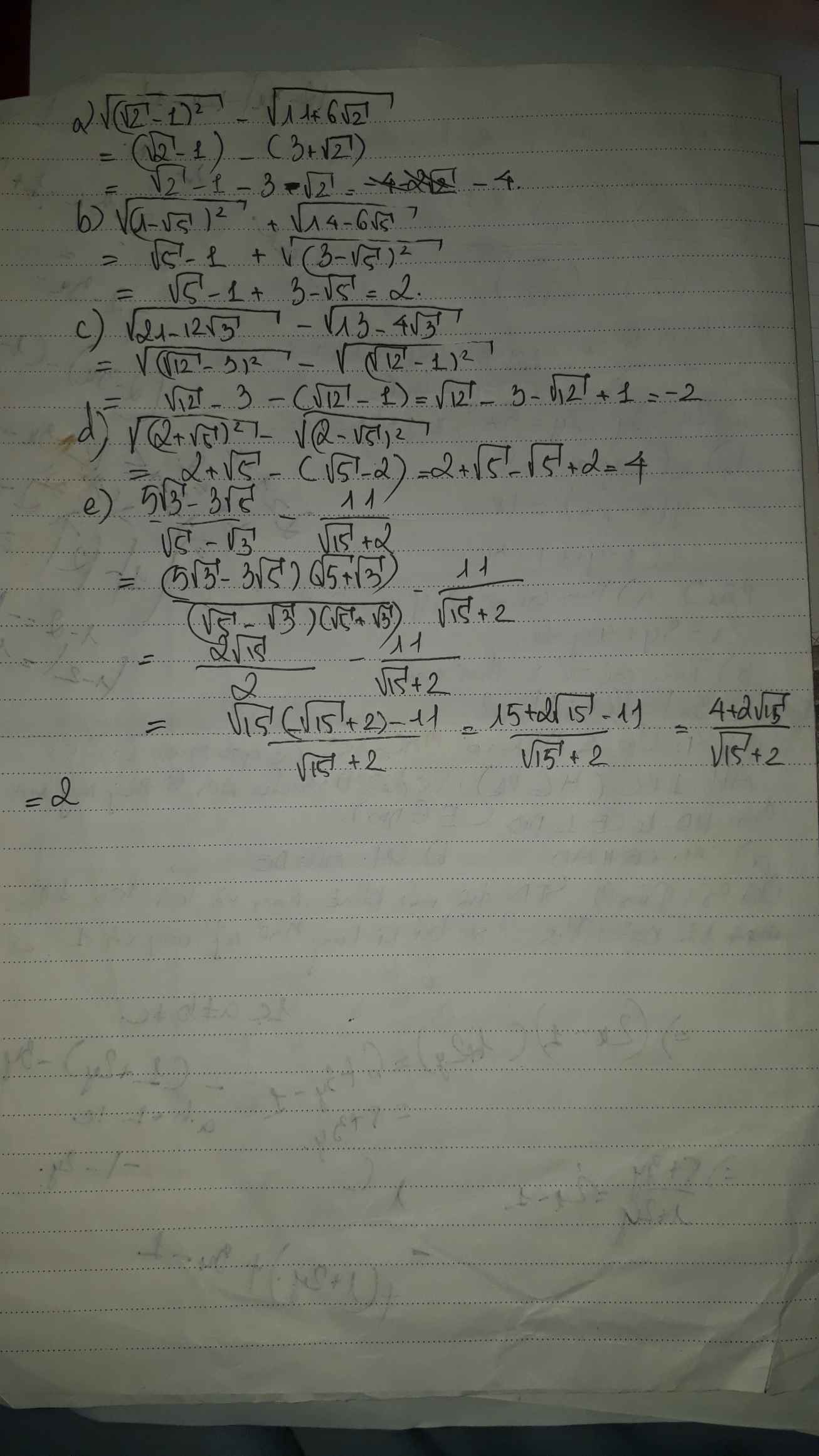
 Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.
Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.
`\sqrt{17-12\sqrt{2}}`
`=\sqrt{17-6.\sqrt{4}.\sqrt{2}}`
`=\sqrt{17-6\sqrt{8}}`
`=\sqrt{9-2.3.\sqrt{8}+8}`
`=\sqrt{(3-\sqrt{8})^{2}}`
`=|3-\sqrt{8}|`
`=3-\sqrt{8}` ( Vì `3=\sqrt{9}>\sqrt{8}` )