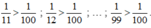K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Cho A = 1/1×2 + 1/3×4 + 1/5×6 +...+ 1/217×218 và B = 1/110 + 1/111 + 1/112 +...+ 1/218
So sánh A và B
0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 3 2024
A = \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{217.218}\)
A = \(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{217}-\dfrac{1}{218}\)
A = 1 - \(\dfrac{1}{218}\)
B = \(\dfrac{1}{110}\) + \(\dfrac{1}{111}\) + \(\dfrac{1}{112}\) + ... + \(\dfrac{1}{218}\)
Xét dãy số 110; 111; 112; ...; 218, dãy số này có số số hạng là:
(218 - 110) : 1 + 1 = 109 (số)
Mặt khác \(\dfrac{1}{110}\) > \(\dfrac{1}{111}>\dfrac{1}{112}>...>\dfrac{1}{218}\)
⇒ B = \(\dfrac{1}{110}\) + \(\dfrac{1}{111}\) + \(\dfrac{1}{112}+...+\dfrac{1}{218}\) < \(\dfrac{1}{110}\) + \(\dfrac{1}{110}\)+ ... +\(\dfrac{1}{110}\)
B < \(\dfrac{1}{110}\) x 109
B < 1 - \(\dfrac{1}{110}\)
\(\dfrac{1}{128}\) < \(\dfrac{1}{110}\) ⇒ A = 1 - \(\dfrac{1}{128}\) > 1 - \(\dfrac{1}{110}\) > B
A > B
PT
1
CM
1 tháng 9 2017
C = 1 10 + 1 11 + 1 12 + ... + 1 99 + 1 100 > 1 ⇔ C = 1 10 + 1 11 + 1 12 + ... + 1 20 + 1 21 + 1 22 + ... + 1 30 + ... + 1 91 + 1 92 + ... + 1 100 C > 1 10 + 10 20 + 10 30 + ... + 10 100 > 10 20 + 10 30 + 10 60 = 1 2 + 1 3 + 1 6 = 1
PT
1
CM
20 tháng 3 2017
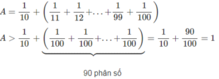
C = 1 10 + 1 11 + ... + 1 100 > 1 10 + 1 100 = ... + 1 100 ⏟ 90 s o = 1 10 + 90 100 = 1
NN
0
CM
26 tháng 1 2017
a) A > 1 20 + 1 20 + ... + 1 20 ⏟ 10 s o = 10 20 = 1 2 .
b) B = 1 5 + ... 1 9 + 1 10 + ... + 1 17 < 1 5 + ... + 1 5 ⏟ 5s o + 1 8 + ... + 1 8 ⏟ 8s o = 2
c) C = 1 10 + 1 11 + 1 12 ... + 1 18 + 1 19 < 1 10 + 1 10 + ... 1 10 ⏟ 9 s o = 1
PT
1
PT
1
CM
20 tháng 11 2018
A = 1 10 + 1 11 + 1 12 + ... + 1 99 + 1 100 = 1 10 + 1 11 + 1 12 + ... + 1 90 + 1 91 + 1 92 + ... 1 99 + 1 100
Đặt A 1 = 1 10 + 1 11 + 1 12 + ... + 1 90 ; A 2 = 1 91 + 1 92 + ... 1 99 + 1 100
Ta có 1 10 > 1 90 ; 1 11 > 1 90 ; 1 12 > 1 90 ; ... ; 1 89 > 1 90
A 1 = 1 10 + 1 11 + 1 12 + ... + 1 90 > 81 ⋅ 1 90
A 1 = 1 10 + 1 11 + 1 12 + ... + 1 90 > 81 ⋅ 1 90
Tương tự 1 91 > 1 100 ; 1 92 > 1 100 ; ... ; 1 99 > 1 100
A 2 = 1 91 + 1 92 + ... 1 99 + 1 100 > 10 ⋅ 1 100
A 2 = 1 91 + 1 92 + ... 1 99 + 1 100 > 10 100 = 1 10
A = 1 10 + 1 11 + 1 12 + ... + 1 99 + 1 100 = A 1 + A 2 > 9 10 + 1 10
A = 1 10 + 1 11 + 1 12 + ... + 1 99 + 1 100 > 1