Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\dfrac{-1}{-4}\)=\(\dfrac{1}{4}>0\)
\(\dfrac{3}{-4}< 0\)
\(\Rightarrow\dfrac{1}{4}>\dfrac{3}{-4}hay\dfrac{-1}{-4}>\dfrac{3}{-4}\)
b) Ta có:
\(\dfrac{15}{17}=1-\dfrac{2}{17}\\ \)
\(\dfrac{25}{27}=1-\dfrac{2}{27}\\ \\ \)
Mà \(\dfrac{2}{17}>\dfrac{2}{27}\left(17< 27\right)\)
\(\Rightarrow1-\dfrac{2}{17}< 1-\dfrac{2}{27}\)hay \(\dfrac{15}{17}< \dfrac{25}{27}\)

Giải:
\(a,\dfrac{23}{28}\) và \(\dfrac{24}{27}.\)
Dùng cách chọn phân số trung gian, ta được phân số: \(\dfrac{23}{27}.\)
Ta có:
\(\dfrac{23}{28}< \dfrac{23}{27}._{\left(1\right)}\)
\(\dfrac{23}{27}< \dfrac{24}{27}._{\left(2\right)}\)
Từ \(_{\left(1\right)}\) và \(_{\left(2\right)}\) suy ra: \(\dfrac{23}{28}< \dfrac{24}{27}.\)
Vậy.....
\(b,\dfrac{12}{25}\) và \(\dfrac{25}{49}.\)
Do 2 phân số này đều xấp xỉ bằng \(\dfrac{1}{2}\) cho nên ta chọn phân số trung gian là \(\dfrac{1}{2}.\)
Ta có:
\(\dfrac{12}{25}< \dfrac{12}{24}=\dfrac{1}{2}.\)
\(\dfrac{25}{49}>\dfrac{25}{50}=\dfrac{1}{2}.\)
\(\Rightarrow\) \(\dfrac{12}{25}< \dfrac{25}{49}.\)
Vậy.....

Ta có: \(\dfrac{20}{39}>\dfrac{20}{41}>\dfrac{18}{41}\left(1\right)\)
\(\dfrac{22}{27}>\dfrac{22}{29}\left(2\right)\)
\(\dfrac{18}{43}=1-\dfrac{25}{43};\dfrac{14}{39}=1-\dfrac{25}{39}\)
Vì \(\dfrac{25}{43}< \dfrac{25}{39}\Rightarrow1-\dfrac{25}{43}>1-\dfrac{25}{39}\Rightarrow\dfrac{18}{43}>\dfrac{14}{39}\left(3\right)\)
Từ \(\left(1\right);\left(2\right);\left(3\right)\) ta suy ra : A>B

Theo quy ước với mọi phân số lớn hơn 0 thì ta có:
\(\dfrac{a}{b}>0=>\dfrac{a}{b}< \dfrac{a+n}{b+n}\left(n\in N;n\ne0\right)\)
Áp dụng với bài trên ta => ĐPCM
CHÚC BẠN HỌC TỐT.......

a) \(\dfrac{3}{4}+\dfrac{3}{5}-\dfrac{18}{60}\) ( MTC: 60)
= \(\dfrac{3.15}{4.15}+\dfrac{3.12}{5.12}-\dfrac{18}{60}\)
= \(\dfrac{45}{60}+\dfrac{36}{60}-\dfrac{18}{60}\)
= \(\dfrac{45+36-18}{60}\)=\(\dfrac{63}{60}=\dfrac{21}{20}\)
b)\(\dfrac{17}{8}-\dfrac{11}{6}-\dfrac{2}{9}\) (MTC:72)
=\(\dfrac{17.9}{8.9}-\dfrac{11.12}{6.12}-\dfrac{2.8}{9.8}\)
= \(\dfrac{153}{72}-\dfrac{132}{72}-\dfrac{16}{72}\)
=\(\dfrac{153-132-16}{72}\)
=\(\dfrac{5}{72}\)
c)\(\dfrac{23}{29}+\dfrac{5}{11}+\dfrac{17}{11}\) (MTC:319)
= \(\dfrac{23.11}{29.11}+\dfrac{5.29}{11.29}+\dfrac{17.29}{11.29}\)
=\(\dfrac{253}{319}+\dfrac{145}{319}+\dfrac{493}{319}\)
=\(\dfrac{253+145+493}{319}\)=\(\dfrac{891}{319}=\dfrac{81}{29}\)
c) \(\dfrac{20}{45}+\dfrac{14}{35}+\dfrac{32}{44}\)
= \(\dfrac{4}{9}+\dfrac{2}{5}+\dfrac{8}{11}\)(Rút gọn b/thức)(MTC:495)
=\(\dfrac{4.55}{9.55}+\dfrac{2.99}{5.99}+\dfrac{8.45}{11.45}\)
=\(\dfrac{220}{495}+\dfrac{198}{495}+\dfrac{360}{495}\)
=\(\dfrac{220+198+360}{495}\)=\(\dfrac{778}{495}\)
e)\(17\dfrac{25}{27}+3\dfrac{7}{2}\)
= \(\dfrac{484}{27}+\dfrac{13}{2}\) (MTC:54)
=\(\dfrac{484.2}{27.2}+\dfrac{13.27}{2.27}\)
\(=\dfrac{968}{54}+\dfrac{351}{54}\)
=\(\dfrac{968+351}{54}=\dfrac{1319}{54}\)

a)\(\dfrac{1212}{2323}=\dfrac{1212:101}{2323:101}=\dfrac{12}{23}\)
b)\(\dfrac{-3435}{4141}< \dfrac{-3434}{4141}=\dfrac{-3434:101}{4141:101}\)
Nhận xét:
\(\dfrac{\overline{abab}}{\overline{cdcd}}=\dfrac{\overline{ab}}{\overline{cd}}\)

2)
S = \(\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{43.46}\)
S = 3 . (\(\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{43.46}\))
S = 1 . (\(\dfrac{1}{1.4}+\dfrac{1}{4.7}+...+\dfrac{1}{43.46}\))
S = 1 . (\(1-\dfrac{1}{4}+...+\dfrac{1}{43}-\dfrac{1}{46}\))
S = 1 . (\(1-\dfrac{1}{46}\))
S = 1 . \(\dfrac{45}{46}\)
S = \(\dfrac{45}{46}\)
=> \(\dfrac{45}{46}\) < 1
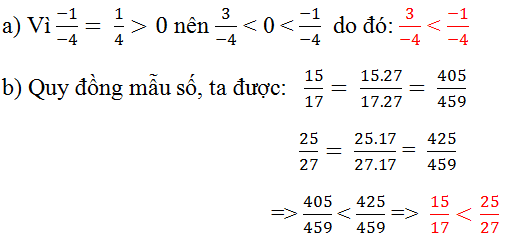
a) Ta có: \(\dfrac{23}{27}>\dfrac{23}{29}\) (1)
\(\dfrac{23}{29}>\dfrac{22}{29}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{23}{27}>\dfrac{22}{29}\)
Vậy \(\dfrac{23}{27}>\dfrac{22}{29}.\)
b) Ta có: \(\dfrac{25}{29}>\dfrac{25}{50}\) (1)
\(\dfrac{25}{50}>\dfrac{12}{25}=\dfrac{24}{50}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{25}{29}>\dfrac{12}{25}\)
Vậy \(\dfrac{25}{29}>\dfrac{12}{25}.\)