Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) Ta có: \(13A=\dfrac{13^{16}+13}{13^{16}+1}=1+\dfrac{12}{13^{16}+1}\)
\(13B=\dfrac{13^{17}+13}{13^{17}+1}=1+\dfrac{12}{13^{17}+1}\)
Vì \(\dfrac{12}{13^{16}+1}>\dfrac{12}{13^{17}+1}\Rightarrow1+\dfrac{12}{13^{16}+1}>1+\dfrac{12}{13^{17}+1}\)
\(\Rightarrow13A>13B\)
\(\Rightarrow A>B\)
Vậy A > B
b) Ta có: \(1999C=\dfrac{1999^{2000}+1999}{1999^{2000}+1}=1+\dfrac{1998}{1999^{2000}+1}\)
\(1999D=\dfrac{1999^{1999}+1999}{1999^{1999}+1}=1+\dfrac{1998}{1999^{1999}+1}\)
\(\dfrac{1998}{1999^{2000}+1}< \dfrac{1998}{1999^{1999}+1}\Rightarrow1+\dfrac{1998}{1999^{2000}+1}< 1+\dfrac{1999}{1999^{1999}+1}\)
\(\Rightarrow1999C< 1999D\)
\(\Rightarrow C< D\)
Vậy C < D

a) \(5\dfrac{4}{23}.27\dfrac{3}{47}+4\dfrac{3}{47}.\left(-5\dfrac{4}{23}\right)\)
\(=5\dfrac{4}{23}.27\dfrac{3}{47}+\left(-4\dfrac{3}{47}\right).5\dfrac{4}{23}\)
\(=5\dfrac{4}{23}.\left[27\dfrac{3}{47}+\left(-4\dfrac{3}{47}\right)\right]\)
\(=5\dfrac{4}{23}.\left(27\dfrac{3}{47}-4\dfrac{3}{27}\right)\)
\(=5\dfrac{4}{23}.23\)
\(=\dfrac{119}{23}.23\)
\(=\dfrac{119}{23}\)
b) \(4.\left(\dfrac{-1}{2}\right)^3+\dfrac{3}{2}\)
\(=4.\dfrac{-1}{6}+\dfrac{3}{2}\)
\(=\dfrac{-4}{6}+\dfrac{3}{2}\)
\(=\dfrac{-2}{3}+\dfrac{3}{2}\)
\(=\dfrac{-4}{6}+\dfrac{9}{6}\)
\(=\dfrac{5}{6}\)
c) \(\left(\dfrac{1999}{2011}-\dfrac{2011}{1999}\right)-\left(\dfrac{-12}{1999}-\dfrac{12}{2011}\right)\)
\(=\dfrac{1999}{2011}-\dfrac{2011}{1999}-\dfrac{-12}{1999}+\dfrac{12}{2011}\)
\(=\left(\dfrac{1999}{2011}+\dfrac{12}{2011}\right)-\left(\dfrac{2011}{1999}+\dfrac{-12}{1999}\right)\)
\(=\dfrac{2011}{2011}-\dfrac{1999}{1999}\)
\(=1-1\)
\(=0\)
d) \(\left(\dfrac{-5}{11}+\dfrac{7}{22}-\dfrac{-4}{33}-\dfrac{5}{44}\right):\left(\dfrac{381}{22}-39\dfrac{7}{22}\right)\)
(đợi đã, mình chưa tìm được hướng làm...)

\(\dfrac{-14}{21};\dfrac{-2}{15};\dfrac{14}{-35}\)
\(\dfrac{-17}{21}=\dfrac{-85}{105}\);\(\dfrac{-2}{15}=\dfrac{-14}{105};\dfrac{14}{-35}=\dfrac{-14}{35}=\dfrac{-42}{105}\)
\(\dfrac{17}{60};\dfrac{5}{12};\dfrac{64}{90}\)
\(\dfrac{17}{60}=\dfrac{51}{180};\dfrac{-5}{12}=\dfrac{-75}{180};\dfrac{-64}{90}=\dfrac{-32}{45}=\dfrac{-128}{180}\)
bài2:
a)\(\dfrac{3}{5}>\dfrac{4}{7}\)
b)\(\dfrac{-5}{8}< \dfrac{-7}{12}\)
c)\(\dfrac{5}{-3}< \dfrac{-9}{12}\)

Đây này má Ran mori
a) \(\left(5\dfrac{1}{7}-3\dfrac{3}{11}\right)-2\dfrac{1}{7}-1\dfrac{8}{11}\)
\(=5+\dfrac{1}{7}-3-\dfrac{3}{11}-2-\dfrac{1}{7}-1-\dfrac{8}{11}\)
\(=\left(5-3-2-1\right)+\left(\dfrac{1}{7}-\dfrac{3}{11}-\dfrac{1}{7}-\dfrac{8}{11}\right)\)
\(=-1+\left(\dfrac{1}{7}-\dfrac{1}{7}\right)-\left(\dfrac{3}{11}+\dfrac{8}{11}\right)\)
\(=-1+0-1=-2\)
a)\(\left(5\dfrac{1}{7}-3\dfrac{3}{11}\right)-2\dfrac{1}{7}-1\dfrac{8}{11}\)
= \(\left(5+\dfrac{1}{7}-3+\dfrac{3}{11}\right)-2+\dfrac{1}{7}-1+\dfrac{8}{11}\)
= \(5-\dfrac{1}{7}+3-\dfrac{3}{11}-2+\dfrac{1}{7}-1+\dfrac{8}{11}\)
= \(\left(5-3-2-1\right)+\dfrac{1}{7}+\dfrac{1}{7}+\dfrac{8}{11}-\dfrac{3}{11}\)
= \(-1+2+\dfrac{5}{11}\)
= \(1+\dfrac{5}{11}=\dfrac{1}{1}+\dfrac{5}{11}=\dfrac{11}{11}+\dfrac{5}{11}=\dfrac{16}{11}\)
Vậy :câu a) = \(\dfrac{16}{11}\)

a) \(\dfrac{-1}{-4}\)=\(\dfrac{1}{4}>0\)
\(\dfrac{3}{-4}< 0\)
\(\Rightarrow\dfrac{1}{4}>\dfrac{3}{-4}hay\dfrac{-1}{-4}>\dfrac{3}{-4}\)
b) Ta có:
\(\dfrac{15}{17}=1-\dfrac{2}{17}\\ \)
\(\dfrac{25}{27}=1-\dfrac{2}{27}\\ \\ \)
Mà \(\dfrac{2}{17}>\dfrac{2}{27}\left(17< 27\right)\)
\(\Rightarrow1-\dfrac{2}{17}< 1-\dfrac{2}{27}\)hay \(\dfrac{15}{17}< \dfrac{25}{27}\)
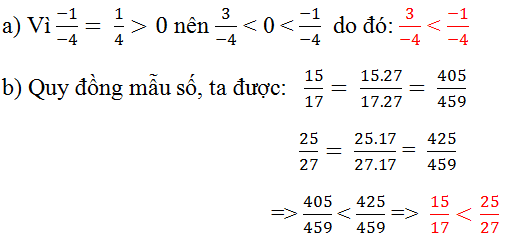
a, \(\dfrac{1998}{1999}\) < \(\dfrac{1999}{2000}\)
b, \(\dfrac{47}{15}>\dfrac{29}{35}\)
c, \(\dfrac{12}{25}< \) \(\dfrac{25}{49}\)