Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là A
Gọi cạnh đáy, cạnh bên của hình hộp đứng lần lượt là x và y ( x ,y > 0)
Ta có:
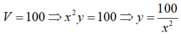
Khi đó:
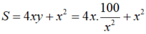
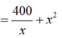
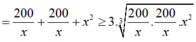
![]()
Vậy S đạt giá trị nhỏ nhất bằng 30 40 3 khi
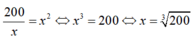

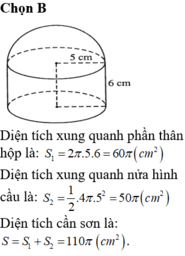
Chọn D
Hình hộp có đáy là hình vuông cạnh: 12 - 2x
Chiều cao của hình hộp là: x
Thể tích hình hộp là y = x ( 12 - 2 x ) 2
Bài toán đưa về tìm x ∈ (0; 6) để hàm số y = f ( x ) = x ( 12 - 2 x ) 2 có giá trị lớn nhất.
y ' = 1 ( 12 - 2 x ) 2 + x . 2 . ( 12 - 2 x ) . ( - 2 )
12 x 2 - 96 x + 144 ;
y' xác định ∀ x ∈ (0; 6)
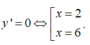
Bảng biến thiên
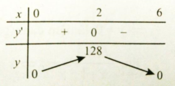
Hàm số đạt giá trị lớn nhất tại x=2

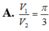



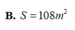


Gọi cạnh đáy là \(a\) , chiều cao là \(h\)
Diện tích đáy là: \(a2\).
Diện tích xung quanh là: \(4ah\)
Ta có:\(V=a^2.h=4\Rightarrow ah=\dfrac{4}{a}\left(\cdot\right)\)
Lượng vàng cần phải dùng là: \(a^2+4ah=a^2+\dfrac{16}{a}\)
Xét hàm số \(f\left(a\right)=a^2+\dfrac{16}{a};a>0\)
Ta có: \(f'\left(a\right)=2a-\dfrac{16}{a^2}\)
\(f'\left(a\right)=0\Leftrightarrow2a-\dfrac{16}{a^2}=0\Leftrightarrow\dfrac{2a^3-16}{a}=0\Leftrightarrow a=2\)
Lập bảng biến thiên ta thấy hàm số \(f\left(a\right)\) đạt giá trị nhỏ nhất tại \(a=2\), thay vào \(\left(\cdot\right)\) suy ra \(h=1\)
Gọi cạnh đáy là a, chiều cao là h.
Diện tích đáy là: a2.
Diện tích xung quanh là: 4ah
Ta có:V=a2h=4⇒ah=4a(∗)
Lượng vàng cần phải dùng là: a2+4ah=a2+16a
Xét hàm số f(a)=a2+16a,a>0
Ta có: f′(a)=2a−16a2
f′(a)=0⇔2a−16a2=0⇔2a3−16a2=0⇔a=2
Lập bảng biến thiên ta thấy hàm số f(a) đạt giá trị nhỏ nhất tại a=2, thay vào (*) suy ra h=1.