K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
14 tháng 7 2023
$\sin \alpha =2$?? $\sin \alpha \in [-1;1]$ với mọi $\alpha$ mà bạn. Bạn xem lại đề.
13 tháng 9 2023
2tan a-cot a=1
=>2tana-1/tan a=1
=>\(\dfrac{2tan^2a-1}{tana}=1\)
=>2tan^2a-tana-1=0
=>(tan a-1)(2tana+1)=0
=>tan a=-1/2 hoặc tan a=1
\(P=\dfrac{tan\left(-a\right)+2\cdot cota}{3\cdot tan\left(\dfrac{pi}{2}+a\right)}=\dfrac{-tana+2\cdot cota}{-3\cdot cota}\)
TH1: tan a=-1/2
\(P=\dfrac{\dfrac{1}{2}+2\cdot\left(-2\right)}{-3\cdot\left(-2\right)}=-\dfrac{7}{2}:6=-\dfrac{7}{12}\)
TH2: tan a=1
=>cot a=1
\(P=\dfrac{-1+2}{-3}=\dfrac{1}{-3}=-\dfrac{1}{3}\)
14 tháng 9 2023
Ta có :
\(2tan\alpha-cot\alpha=1\)
\(\Leftrightarrow2tan\alpha-\dfrac{1}{tan\alpha}=1\)
\(\Leftrightarrow2tan\alpha-\dfrac{1}{tan\alpha}-1=0\)
\(\Leftrightarrow\dfrac{2tan^2\alpha-tan\alpha-1}{tan\alpha}=0\left(tan\alpha\ne0\right)\)
\(\Leftrightarrow2tan^2\alpha-tan\alpha-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tan\alpha=1\\tan\alpha=-\dfrac{1}{2}\end{matrix}\right.\)
\(P=\dfrac{tan\left(8\pi-\alpha\right)+2cot\left(\pi+\alpha\right)}{3tan\left(\dfrac{3\pi}{2}+\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{tan\left(4.2\pi-\alpha\right)+2cot\alpha}{3tan\left(2\pi-\dfrac{\pi}{2}+\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{tan\left(-\alpha\right)+2cot\alpha}{3tan\left[-\left(\dfrac{\pi}{2}-\alpha\right)\right]}\)
\(\Leftrightarrow P=\dfrac{-tan\alpha+2cot\alpha}{-3tan\left(\dfrac{\pi}{2}-\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{-tan\alpha+2cot\alpha}{-3cot\alpha}\)
- Với \(tan\alpha=1\Rightarrow cot\alpha=1\)
\(\Leftrightarrow P=\dfrac{-1+2.1}{-3.1}=-\dfrac{1}{3}\)
- Với \(tan\alpha=-\dfrac{1}{2}\Rightarrow cot\alpha=-2\)
\(\Leftrightarrow P=\dfrac{\dfrac{1}{2}+2.\left(-2\right)}{-3.\left(-2\right)}=\dfrac{-\dfrac{7}{2}}{6}=-\dfrac{7}{12}\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có α + β = π nên sinα = sin(π – α) = sinβ, suy ra sin2α = sin2β.
a) A = sin2α + cos2β = sin2β + cos2β = 1.
b) Ta có α + β = π nên cosα = – cos(π – α) = – cosβ.
Khi đó, B = (sinα + cosβ)2 + (cosα + sinβ)2
= (sinβ + cosβ)2 + (– cosβ + sinβ)2
= (sinβ + cosβ)2 + (sinβ – cosβ )2
= sin2β + 2sinβ cosβ + cos2β + sin2β – 2sinβ cosβ + cos2β
= 2(sin2β + cos2β)
= 2 . 1 = 2.
PT
1
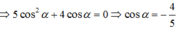
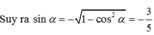
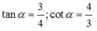
\(tana+cota=2\Leftrightarrow\frac{sina}{cosa}+\frac{cosa}{sina}=2\)
\(\Leftrightarrow\frac{sin^2a+cos^2a}{sina.cosa}=2\)
\(\Leftrightarrow1=2sina.cosa\)
\(\Leftrightarrow sin2a=1\)