
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

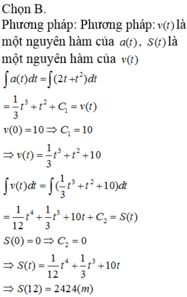

6.
d nhận \(\left(2;-1;-3\right)\) là 1 vtcp
7.
Phương trình mặt phẳng (P) qua A và vuông góc d nhận \(\left(3;2;-1\right)\) là 1 vtpt có dạng:
\(3\left(x-4\right)+2\left(y+3\right)-1\left(z-2\right)=0\)
\(\Leftrightarrow3x+2y-z-4=0\)
Pt tham số d: \(\left\{{}\begin{matrix}x=-2+3t\\y=-2+2t\\z=-t\end{matrix}\right.\)
A' là giao điểm d và (P) nên tọa độ thỏa mãn:
\(3\left(-2+3t\right)+2\left(-2+2t\right)+t-4=0\Rightarrow t=1\)
\(\Rightarrow A'\left(1;0;-1\right)\)
8.
Tọa độ H là \(H\left(0;2;0\right)\) (giữ tung độ, thay hoành độ và cao độ bằng 0 là xong)
4.
\(\left(1+e^x\right)x=\left(1+e\right)x\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Diện tích:
\(S=\int\limits^1_0\left[\left(1+e\right)x-\left(1+e^x\right)x\right]dx\)
\(=\int\limits^1_0e.xdx-\int\limits^1_0x.e^xdx\)
\(=\left(\frac{1}{2}e.x^2-\left(x-1\right)e^x\right)|^1_0=\frac{e}{2}-1=\frac{e-2}{2}\)
5.
Do 3 điểm A;B;C lần lượt thuộc 3 trục tọa độ nên mặt cầu đi qua 4 điểm có tâm \(I\left(\frac{1}{2};-1;2\right)\)
\(R=IA=\sqrt{\left(\frac{1}{2}\right)^2+\left(-1\right)^2+2^2}=\frac{\sqrt{21}}{2}\)
Phương trình:
\(\left(x-\frac{1}{2}\right)^2+\left(y+1\right)^2+\left(z-2\right)^2=\frac{21}{4}\)

Chọn B
Quãng đường một vật di chuyển trong khoảng thời gian từ thời điểm t = t0 (s) đến thời điểm t = t1 (s) với vận tốc v(t) (m/s) được tính theo công thức s = ∫ t 0 t 1 v t d t . Ở đậy vận tốc v(t) là nguyên hàm của gia tốc a(t).

3.
\(x^2+4y^2=x^2+8.\frac{y^2}{2}\ge9\sqrt[9]{\frac{x^2y^{16}}{2^8}}\)
\(\Rightarrow\sqrt{x^2+4y^2}\ge\sqrt{9\sqrt[9]{\frac{x^2y^{16}}{2^8}}}=3\sqrt[9]{\frac{xy^8}{2^4}}\)
\(\Rightarrow x+\sqrt{x^2+4y^2}\ge x+3\sqrt[9]{\frac{xy^8}{2^4}}\ge4\sqrt[4]{x\sqrt[3]{\frac{xy^8}{2^4}}}=4\sqrt[12]{\frac{x^4y^8}{2^4}}=4\sqrt[3]{\frac{xy^2}{2}}\)
\(\Rightarrow\left(x+\sqrt{x^2+4y^2}\right)^3\ge\left(4\sqrt[3]{\frac{xy^2}{2}}\right)^3=32xy^2\)
\(\Rightarrow P\le\frac{4xy^2}{32xy^2}=\frac{1}{8}\)
\(P_{max}=8\) khi \(y=x\sqrt{2}\)
4.
\(y'=x^2+2\left(m+1\right)x+4\) (1)
Để hàm số nghịch biến trên 1 đoạn có độ dài bằng \(2\sqrt{5}\)
\(\Leftrightarrow\left(1\right)\) có 2 nghiệm pb thỏa mãn \(\left|x_2-x_1\right|=2\sqrt{5}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m+1\right)^2-4>0\\\left(x_2-x_1\right)^2=20\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m^2+2m-3>0\\\left(x_1+x_2\right)^2-4x_1x_2=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>1\\m< -3\end{matrix}\right.\\4\left(m+1\right)^2-16=20\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=2\\m=-4\end{matrix}\right.\)
\(\Rightarrow\sum m=-2\)
5.
Pt đoạn chắn: \(\frac{x}{2}+\frac{y}{-3}+\frac{z}{4}=1\Leftrightarrow6x-4y+3z+12=0\)
Mặt phẳng (MNP) nhận \(\left(6;-4;3\right)\) là 1 vtpt
1.
\(v\left(t\right)=s'\left(t\right)=-3t^2+12t+17=-3\left(t-2\right)^2+29\le29\)
\(\Rightarrow v\left(t\right)_{max}=29\) khi \(t=2\left(s\right)\)
2.
E là trung điểm AD \(\Rightarrow ABCE\) là hình vuông
Gọi O là giao điểm AC và BE, qua O kẻ đường thẳng song song SA cắt SC tại I
\(\Rightarrow\) I là tâm mặt cầu ngoại tiếp S.ABCE
\(\Rightarrow R=IC=\frac{SC}{2}\)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\) \(\Rightarrow SC=\sqrt{SA^2+AC^2}=2a\)
\(\Rightarrow R=\frac{AC}{2}=a\)

Vận tóc của chuyển động là:
\(v=s'=12t-3t^2\)
Ta có \(v'=12-6t\)
\(v'=0\) khi t = 2 và \(v'\) đổi dấu từ dương sang âm khi đi qua t=2. Vậy \(v\) đạt giá trị lớn nhất khi t = 2.

16.
\(\overrightarrow{n_{\left(P\right)}}=\left(2;1;-1\right)\) ; \(\overrightarrow{n_{\left(Q\right)}}=\left(1;-2;1\right)\)
\(\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{n_{\left(Q\right)}}\right]=\left(-1;-3;-5\right)\)
\(\Rightarrow\) Giao tuyến 2 mp nhận \(\left(-1;-3;-5\right)\) hoặc \(\left(1;3;5\right)\) là 1 vtcp
17.
Đường thẳng nhận \(\left(2;-3;6\right)\) là 1 vtcp
Pt tham số: \(\left\{{}\begin{matrix}x=-2+2t\\y=4-3t\\z=3+6t\end{matrix}\right.\)
Pt chính tắc: \(\frac{x+2}{2}=\frac{y-4}{-3}=\frac{z-3}{6}\)
18.
Pt tham số đường thẳng d qua A và vuông góc (P): \(\left\{{}\begin{matrix}x=-2+t\\y=1+t\\z=5-t\end{matrix}\right.\)
H là giao điểm d và (P) nên tọa độ thỏa mãn:
\(-2+t+1+t-5+t+9=0\Rightarrow t=-1\) \(\Rightarrow H\left(-3;0;6\right)\)
19.
Pt mặt phẳng (P) qua A và vuông góc d:
\(3\left(x-4\right)+2\left(y+3\right)-z=0\)
\(\Leftrightarrow3x+2y-z-6=0\)
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=-2+3t\\y=-2+2t\\z=-t\end{matrix}\right.\)
H là giao điểm d và (P) nên tọa độ thỏa mãn:
\(3\left(-2+3t\right)+2\left(-2+2t\right)+t=0\Rightarrow t=\frac{5}{7}\) \(\Rightarrow H\left(\frac{1}{7};-\frac{4}{7};-\frac{5}{7}\right)\)
14.
\(\overrightarrow{BA}=\left(4;2;0\right)=2\left(2;1;0\right)\)
Gọi M là trung điểm AB \(\Rightarrow M\left(-1;1;-1\right)\)
Mp trung trực AB vuông góc AB và qua M có pt:
\(2\left(x+1\right)+1\left(y-1\right)=0\Leftrightarrow2x+y+1=0\)
15.
Gọi pt \(\left(Q\right)\) có dạng \(ax+by+cz+d=0\) (\(d\ne0\))
(Q) qua A nên: \(2a+d=0\) \(\Rightarrow d=-2a\)
\(\left(P\right)\perp\left(Q\right)\Leftrightarrow2b-c=0\) \(\Rightarrow c=2b\)
\(d\left(O;\left(Q\right)\right)=\frac{4}{3}\Leftrightarrow\frac{\left|d\right|}{\sqrt{a^2+b^2+c^2}}=\frac{4}{3}\Leftrightarrow9d^2=16\left(a^2+b^2+c^2\right)\) \(\Leftrightarrow36a^2=16\left(a^2+b^2+4b^2\right)\) \(\Leftrightarrow20a^2=80b^2\Leftrightarrow\left[{}\begin{matrix}a=2b\\a=-2b\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}a=2;b=1;c=2;d=-4\\a=2;b=-1;c=-2;d=-4\end{matrix}\right.\) Có 2 mặt phẳng (Q) thỏa mãn: \(\left[{}\begin{matrix}2x+y+2z-4=0\\2x-y-2z-4=0\end{matrix}\right.\)

14.
Pt mp (P) qua A và vuông góc d:
\(1\left(x-2\right)-2\left(y-3\right)+2\left(z+1\right)=0\)
\(\Leftrightarrow x-2y+2z+6=0\)
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=4+t\\y=1-2t\\z=5+2t\end{matrix}\right.\)
Gọi M là giao điểm d và (P) thì tọa độ M thỏa mãn:
\(4+t-2\left(1-2t\right)+2\left(5+2t\right)+6=0\) \(\Rightarrow t=-2\) \(\Rightarrow M\left(2;5;1\right)\)
A' đối xứng A qua d \(\Rightarrow\)M là trung điểm AA'
Theo công thức trung điểm \(\Rightarrow A'\left(2;7;3\right)\)
15.
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=-2+3t\\y=-2+2t\\z=-t\end{matrix}\right.\)
PT (P) qua A và vuông góc d:
\(3\left(x-4\right)+2\left(y+3\right)-1\left(z-2\right)=0\)
\(\Leftrightarrow3x+2y-z-4=0\)
H là giao điểm d và (P) nên tọa độ thỏa mãn:
\(3\left(-2+3t\right)+2\left(-2+2t\right)+t-4=0\Rightarrow t=1\)
\(\Rightarrow H\left(1;0;-1\right)\)
11.
Thay tọa độ 4 điểm vào pt d chỉ có đáp án A thỏa mãn
12.
Phương trình (P) qua A và vuông góc \(\Delta\):
\(1\left(x-0\right)+1\left(y-1\right)-1\left(z+1\right)=0\Leftrightarrow x+y-z-2=0\)
Gọi M là giao điểm d và (P) thì tọa độ M thỏa mãn:
\(1+t+2+t-\left(13-t\right)-2=0\Rightarrow t=4\) \(\Rightarrow M\left(5;6;9\right)\)
\(\Rightarrow\overrightarrow{AM}=\left(5;5;10\right)=5\left(1;1;2\right)\)
Phương trình tham số d: \(\left\{{}\begin{matrix}x=t\\y=1+t\\z=-1+2t\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}x=5+t\\y=6+t\\z=9+2t\end{matrix}\right.\)
13.
Pt tham số đường d qua A vuông góc (P): \(\left\{{}\begin{matrix}x=-t\\y=1-2t\\z=-2+2t\end{matrix}\right.\)
H là giao điểm (P) và d nên tọa độ thỏa mãn:
\(t-2\left(1-2t\right)+2\left(-2+2t\right)-3=0\Rightarrow t=1\)
\(\Rightarrow H\left(-1;-1;0\right)\)