Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì hai túi là khác nhau nên biến cố lấy một viên bi mỗi túi là độc lập.
Gọi biến cố A: “Hai viên bi được lấy có cùng màu xanh”, biến cố B: “Hai viên bi được lấy có cùng màu đỏ”, biến cố C: “Hai viên bi được lấy có cùng màu”
a) Xác suất lấy được viên bi màu xanh từ túi I là \(\frac{3}{{10}}\)
Xác suất lấy được viên bi màu xanh từ túi II là \(\frac{{10}}{{16}} = \frac{5}{8}\)
Xác suất lấy được hai viên bi cùng màu xanh là \(\frac{3}{{10}}.\frac{5}{8} = \frac{3}{{16}}\)
b) Xác suất lấy được viên bi màu đỏ từ túi I là \(\frac{7}{{10}}\)
Xác suất lấy được viên bi màu đỏ từ túi II là \(\frac{6}{{16}} = \frac{3}{8}\)
Xác suất lấy được hai viên bi cùng màu đỏ là \(\frac{7}{{10}}.\frac{3}{8} = \frac{{21}}{{80}}\)
c) Ta có \(C = A \cup B\) mà A và B xung khắc nên
\(P\left( C \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) = \frac{3}{{16}} + \frac{{21}}{{80}} = \frac{9}{{20}}\)
Vậy xác suất để hai viên bi được lấy có cùng màu là \(\frac{9}{{20}}.\)
d) Gọi biến cố D: “Hai viên bi được lấy không cùng màu”
Khi đó \(\overline D = C\)
\( \Rightarrow P\left( D \right) = 1 - P\left( {\overline D } \right) = 1 - P\left( C \right) = 1 - \frac{9}{{20}} = \frac{{11}}{{20}}\)
Vậy xác suất để hai viên bi được lấy không cùng màu là \(\frac{{11}}{{20}}.\)

a: n(omega)=4+3+3+5=15
n(xanh)=4+3=7
=>P=7/15
b: P=7/15*4/7=4/15

a.
Có \(C_{17}^5\) cách lấy 5 viên bi tùy ý từ 17 viên bi
b.
Lấy 1 bi trắng từ 7 bi trắng, 2 bi xanh từ 4 bi xanh và 2 bi đỏ từ 6 bi đỏ
Số cách lấy là: \(C_7^1.C_4^2.C_6^2\) cách
c.
Các trường hợp thỏa mãn: 1 trắng 1 đỏ 3 xanh, 1 trắng 2 đỏ 2 xanh, 1 trắng 3 đỏ 1 xanh, 2 trắng 1 đỏ 2 xanh, 2 trắng 2 đỏ 1 xanh
Số cách lấy là:
\(C_7^1C_6^1C_4^3+C_7^1C_6^2C_4^2+C_7^1C_6^3C_4^1+C_7^2C_6^1C_4^2+C_7^2C_6^2C_4^1\) cách
Thầy có thể giải thích cụ thể hơn về câu a được không thưa thầy?

Các trường hợp xảy ra theo yêu cầu đề:
Trường hơp 1: 2 xanh, 2 vàng, 2 đỏ, có: ![]() cách.
cách.
Trường hợp 2: 2 xanh,1 vàng, 3 đỏ, có: ![]() cách.
cách.
Vậy có : ![]() cách.
cách.
Chọn D.

Sử dụng phương pháp gián tiếp:
Lấy ra 9 viên bi trong 15 viên bi bất kỳ, có C 15 9 cách.
Trường hợp 1: lấy 9 viên bi chỉ có 2 màu là xanh và đỏ, có C 11 9 cách.
Trường hợp 2: lấy 9 viên bi chỉ có 2 màu là xanh và vàng, có C 9 9 cách.
Trường hợp 3: lấy ra 9 viên bi chỉ có màu đỏ và vàng, có C 10 9 cách.
Vậy có : C 15 9 - ( C 11 9 + C 9 9 + C 10 9 ) = 4984 cách.
Chọn C.

Chọn D
Cách 1:
Số phần tử của không gian mẫu: ![]() .
.
Gọi A là biến cố: “lấy ra 4 viên bi có đủ ba màu”
Ta xét các khả năng của biến cố A:
TH1: Lấy được 1 bi trắng, 1 bi xanh và 2 bi vàng, trường hợp này có ![]() (cách).
(cách).
TH2: Lấy được 1 bi trắng, 2 bi xanh và 1 bi vàng, trường hợp này có ![]() (cách).
(cách).
TH3: Lấy được 2 bi trắng, 1 bi xanh và 1 bi vàng, trường hợp này có ![]() (cách).
(cách).
Số cách lấy 4 viên bi có đủ cả ba màu là: ![]()
Xác suất cần tìm là ![]()
Cách 2:
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố: “lấy ra 4 viên bi không có đủ ba màu” .
Ta có: ![]()
Xác suất của biến cố A là: ![]()
Vậy xác suất cần tìm là: 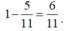 .
.
Đáp án là B
Các viên bi lấy ra có đủ cả 2 màu nên ta có các trường hợp:
Số bi trắng
Số bi xanh
Số cách chọn
1
3
2
3
3
1
Vậy có tất cả cách lấy thỏa mãn yêu cầu bài toán.
C 6 1 . C 5 3 + C 6 2 . C 5 2 + C 6 3 . C 5 1 =310