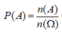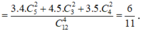Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TH1: 4 viên được lấy chỉ gồm 2 màu đỏ và trắng.
\(\Rightarrow\) Có \(C^4_7\) cách chọn.
TH2: 4 viên được lấy chỉ gồm 2 màu đỏ và vàng.
\(\Rightarrow\) Có \(C^4_8\) cách chọn.
TH3: 4 viên được lấy chỉ gồm 2 màu trắng và vàng.
\(\Rightarrow\) Có \(C^4_9\) cách chọn.
TH2 và TH3 đã bao gồm TH lấy 4 viên chỉ có màu trắng và 4 viên chỉ có màu vàng.
\(\Rightarrow\) Có \(C^4_7+C^4_8+C^4_9-C^4_4-C^4_5=225\) cách chọn ra 4 viên bi không đủ ba màu.

Đáp án D
+ Trường hợp 1: chọn 4 bi đỏ hoặc trắng có ![]() cách
cách
+ Trường hợp 2: chọn 4 bi đỏ và vàng hoặc 4 bi vàng có ![]() cách
cách
+ Trường hợp 3: chọn 3 bi trắng và vàng có ![]() cách
cách
Vậy có ![]() cách
cách

"sao không cho đủ 3 màu" nghĩa là gì bạn? Đủ 3 màu hay không đủ 3 màu?
Chắc là "Sao cho không đủ ba màu"
Nếu em làm là trước hết tìm số cách chọn 4 viên bất kì, sau đó tìm số cách chọn 4 viên có đủ ba màu, sau em lấy cái 4 viên bất kì trừ đi số viên có đủ 3 màu.
Nhưng mà không biết em sai ở đâu chỗ tìm 4 viên có đủ ba màu.
Đoạn này em làm là:
Số cách chọn 4 viên bất kì là: \(C_{15}^4=1365\) cách
Có \(4.5.6\) cách chọn 3 viên ba màu khác nhau, sau đó chọn thêm 1 viên bất kì từ 12 viên còn lại. Sau cùng được \(4.5.6.12=1440\) (vô lí)
Chỉ ra lỗi sai giúp em với ạ.

Chọn D
Cách 1:
Số phần tử của không gian mẫu: ![]() .
.
Gọi A là biến cố: “lấy ra 4 viên bi có đủ ba màu”
Ta xét các khả năng của biến cố A:
TH1: Lấy được 1 bi trắng, 1 bi xanh và 2 bi vàng, trường hợp này có ![]() (cách).
(cách).
TH2: Lấy được 1 bi trắng, 2 bi xanh và 1 bi vàng, trường hợp này có ![]() (cách).
(cách).
TH3: Lấy được 2 bi trắng, 1 bi xanh và 1 bi vàng, trường hợp này có ![]() (cách).
(cách).
Số cách lấy 4 viên bi có đủ cả ba màu là: ![]()
Xác suất cần tìm là ![]()
Cách 2:
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố: “lấy ra 4 viên bi không có đủ ba màu” .
Ta có: ![]()
Xác suất của biến cố A là: ![]()
Vậy xác suất cần tìm là: 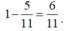 .
.

Chọn D
Chọn ngẫu nhiên 4 viên bi từ hộp có 12 viên bi thì có ![]()
Số cách lấy để được đủ ba màu là ![]()
Xác suất để 4 viên bi lấy ra có đủ ba màu bằng