Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi H là trung điểm của AC. \(\Delta\)DAC cân tại D.
Do đó DH\(\perp\)AC và AH = \(\frac{1}{2}\)AC (1)
Vẽ AK \(\perp\)BC. Vì \(\Delta\)AKC vuông tại K và ^BCA = 300
nên AK = \(\frac{1}{2}\)AC (2)
Từ (1) và (2) suy ra AK = AH
Xét \(\Delta\)AKB và \(\Delta\)AHD có:
^AKB = ^AHD (=900)
AK = AH(gt)
^BAK = ^DAH (=500)
Do đó \(\Delta\)AKB = \(\Delta\)AHD (g.c.g)
=> AB = AD
Vậy \(\Delta\)ABD cân tại A(đpcm)

1.
\(a,\sin\widehat{B}=\sin60^0=\dfrac{AC}{BC}=\dfrac{\sqrt{3}}{2}\Leftrightarrow AC=\dfrac{12\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\\ b,AC^2=CH\cdot BC\left(HTL.\Delta\right)\\ \Rightarrow CH=\dfrac{AC^2}{BC}=9\left(cm\right)\)
Tim Gia Tri Nho Nhat Cua
a) A = x - 4 can x + 9
b) B = x - 3 can x - 10
c ) C = x - can x + 1
d ) D = x + can x + 2

có (x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=0
<=> 3x2-2(a+b+c)x-(ab+bc+ca)=0
vì phương trình có nghiện kép nên denta=0
\(\Delta=4\left(a+b+c\right)^2-12\left(ab+bc+ca\right)\)
\(=4\left(a^2+b^2+c^2-ab-bc-ca\right)\)
do đó \(a^2+b^2+c^2=ab+bc+ca\)
vì a, b, c là độ dài 3 cạnh của tam giác nên
a, b, c là các số dương
nên áp dụng bđt cosi ta có
\(a^2+b^2+c^2\ge ab+bc+ca\)
dấu bằng xảy ra khi a=b=c
vậy tam giác cần tìm là tam giác đều
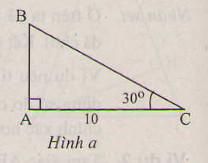
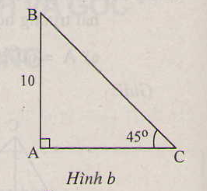
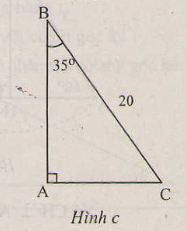
Giả sử BC = AH = a
Vì Δ ABC là tam giác cân nên AH là đường cao đồng thời là đường trung tuyến
=> H là trung điểm BC => HB = HC = B C 2 = a 2
Xét ABH vuông tại H ta có:
Vì ABC là tam giác cân
Ta có A ^ = B ^ = C ^ = 180 0 (định lý tổng ba góc trong một tam giác)
Đáp án cần chọn là: D