Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Có các trường hợp sau:
+ 1 nam, 3 nữ, suy ra có C 18 1 C 17 3 cách gọi
+ 2 nam, 2 nữ, suy ra có C 18 2 C 17 2 cách gọi
+ 3 nam, 1 nữ, suy ra có C 18 3 C 17 1 cách gọi
Suy ra xác suất sẽ bằng
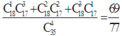

Đáp án B
Có các trường hợp sau:
+ 1 nam, 3 nữ, suy ra có C 18 1 C 17 3 cách gọi
+ 2 nam, 2 nữ, suy ra có C 18 2 C 17 2 cách gọi
+ 3 nam, 1 nữ, suy ra có C 18 3 C 17 1 cách gọi
Suy ra xác suất sẽ bằng
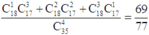

Chọn D
Gọi A là biến cố “4 học sinh được gọi có cả nam và nữ”, suy ra A ¯ là biến cố “4 học sinh được gọi toàn là nam hoặc toàn là nữ”
Số phần tử của không gian mẫu là ![]()
Ta có ![]()
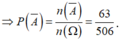
Vậy xác suất của biến cố A là
![]()

Đáp án B
Phương pháp: Xác suất : P ( A ) = n ( A ) n ( Ω )
Cách giải:
Số phần tử của không gian mẫu : n ( Ω ) = C 15 + 10 4 = C 25 4
Gọi A là biến cố : “4 học sinh được gọi đó cả nam lẫn nữ”
Khi đó :
![]()
Xác suất cần tìm:
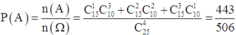

số cách gọi 4 hs lên bảng là: \(C^4_{25}\)Gọi A là biến cố :" bốn hs lên bảng có cả nam và nữ:
=> ta phải tính n(A)=?
phương án 1; 3 nam và 1 nữ: \(C^3_{15}.C^1_{10}=4550\)
phương án 2: 2 nam và 2 nữ : \(C^1_{15}.C^2_{10}=4725\)
phương án 3: 1 nam vfa 3 nữ: \(C^1_{15}.C^3_{10}=1800\)
=> n(A)=4550+4725+1800=11075 cách
=> p(A)=\(\frac{11075}{C^4_{25}}=\frac{443}{506}\)
chue yếu bạn áp dụng các quy tắc cộng và nhân là xong

a) Không gian mẫu của bài toán này là tập hợp các học sinh trong tổ lớp, nó có 9 phần tử và được ký hiệu là Ω = {Hương, Hồng, Dung, Phương, Sơn, Tùng, Hoàng, Tiến, Hải}.
b) Biến cố H xảy ra khi học sinh được chọn là một bạn nữ, nó là tập hợp các học sinh nữ và được ký hiệu là
H = {Hương, Hồng, Dung, Phương}.
Biến cố K xảy ra khi học sinh được chọn có tên bắt đầu là chữ cái H, được ký hiệu là
K = {Hương, Hồng, Hoàng}.
Biến cố hợp M xảy ra khi học sinh được chọn là một bạn nữ hoặc có tên bắt đầu bằng chữ H, nó là tập hợp các học sinh trong tập H hoặc K (bao gồm cả những học sinh trùng nhau của hai tập này) và được ký hiệu là
M = H ∪ K = {Hương, Hồng, Dung, Phương, Hoàng}.
a: Ω={Hương, Hồng, Dung, Phương, Sơn, Tùng, Hoàng, Tiến, Hải}
n(Ω)=9
b: H={Hương, Hồng, Dung, Phương}
K={Hương, Hồng, Hoàng}
=>M={Hương,Hồng,Dung,Phương,Hoàng}
H là tập con của M và Ω
K là tập con của M và Ω
M là tập con của Ω

Chọn A.
Chọn ngẫu nhiên 5 học sinh trong số 48 học sinh có:![]()
- Gọi A là biến cố "chọn 5 học sinh trong đó có ít nhất một học sinh nữ" thì ![]() là biến cố "chọn 5 học sinh mà trong đó không có học sinh nữ".
là biến cố "chọn 5 học sinh mà trong đó không có học sinh nữ".
- Ta có số kết quả thuận lợi cho ![]() là:
là:
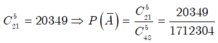
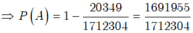

Đáp án A
Cách gọi ngẫu nhiên 2 học sinh lên bảng: C 40 2
Cách gọi 2 học sinh tên Anh lên bảng: C 4 2
⇒ p = C 4 2 C 40 2 = 1 130

Đáp án C
Gọi ngẫu nhiên hai học sinh lên bảng trong 40 học sinh nên ta có: ![]()
Gọi biến cố A: “Trong hai bạn được gọi lên bảng, cả hai bạn đều tên là Anh”.
Trong lớp có 4 bạn tên là Anh nên ta có: ![]()
Khi đó ta có xác suất để hai bạn được gọi lên bảng đều tên là Anh là:  .
.
Không gian mẫu là số cách gọi ngẫu nhiên 2 nam, 2 nữ từ 46 học sinh.
Suy ra số phần tử của không gian mẫu là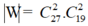 .
.
Gọi A là biến cố 4 học sinh (2 nam, 2 nữ) được gọi lên đều không chuẩn bị bài tập về nhà, trong đó có Bình và Mai . Ta mô tả khả năng thuận lợi cho biến cố A như sau:
● Gọi Bình và Mai lên bảng, có 1 cách.
● Tiếp theo gọi 1 bạn nam từ 6 bạn không làm bài tập về nhà còn lại và 1 bạn nữ từ 3 bạn không làm bài tập về nhà còn lại, có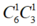 cách.
cách.
Suy ra số phần tử của biến cố A là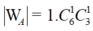 .
.
Vậy xác suất cần tính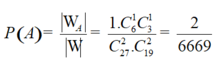 .
.
Chon C.