Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số công nhân ban đầu của tổ đó là x(x>2 x\(\in\)N)
Năng suất mỗi người phải làm theo dự định là: \(\frac{540}{x}\)(sản phẩm)
Do có 2 công nhân phải đi làm việc khác nên số người còn lại là: x-2 (người)
Năng suất thực tế mỗi công nhân phải làm là: \(\frac{540}{x-2}\)(sản phẩm)
Vì thực tế mỗi người phải làm thêm 3 sản phẩm nên ta có phương trình:
\(\frac{540}{x-2}\)-\(\frac{540}{x}\)=3
<=> 540x-540(x-2)=3.x(x-2)
<=> 540x -540x+1080=3\(x^2\)-6x
<=> 3\(x^2\)-6x-1080=0
<=> \(\left[\begin{array}{nghiempt}x=20\\x=-18\left(loại\right)\end{array}\right.\)
vậy ban đầu có 20 công nhân

Gọi năng suất ban đầu là x, thời gian ban đầu là y
Theo đề, ta có hệ: xy=120 và 2x+(x+4)(y-2-1)-16=120
=>xy=120 và 2x+(x+4)(y-3)=136
=>xy=120 và 2x+xy-3x+4y-12=136
=>xy=120 và -x+4y+120-12=136
=>-x+4y=28 và xy=120
=>x=4y-28 và y(4y-28)=120
=>y=10 và x=4*10-28=12

Gọi t1 (giờ) là thời gian người thứ nhất sơn xong bức tường,
t2 (giờ) là thời gian người thứ hai sơn xong bức tường.
(Điều kiện: t1 > 0; t2 > 0)
+ Trong một giờ:
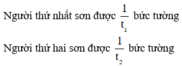
+ Người thứ nhất làm trong 7 giờ và người thứ hai làm trong 4 giờ thì họ sơn được 5/9 bức tường nên ta có: 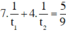
+ Sau đó họ cùng làm việc với nhau trong 4 giờ nữa, nghĩa là người thứ nhất làm trong 7 + 4 = 11 giờ và người thứ hai làm trong 4 + 4 = 8 giờ.
Khi đó họ còn 1/18 bức tường chưa sơn nghĩa là họ đã sơn được 17/18 bức tường.
Ta có phương trình 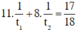
Ta có hệ phương trình 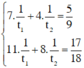
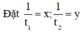 , khi đó hệ phương trình trở thành
, khi đó hệ phương trình trở thành 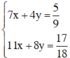
Giải hệ phương trình trên ta được 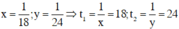
Vậy nếu mỗi người làm riêng thì người thứ nhất sơn xong bức tường trong 18 giờ, người thứ hai sơn xong bức tường trong 24 giờ.

Cả hai ngày đội công nhân làm được là:
2/7+2/3=20/21 (quãng đường)
Vậy...
Cả hai ngày đội công nhân làm được số phần của quãng đường là :
2/7 + 2/3 = 20/21 ( quãng đường )
đáp số : ....

Gọi x là số sản phẩm sản xuất trong một ngày theo định mức.
Điều kiện x nguyên dương. Theo đề ta có chương trình:
\(\dfrac{360}{x}=\dfrac{360+\dfrac{360.5}{100}}{x+9}+1\)
⇔ x2 + 27x – 3240 = 0
⇒ x1= -72 (loại), x2 = 45.
Thời gian giao hoàn thành kế hoạch là = 8 ngày
Nếu sản xuất theo thời gian đã định với năng suất mới thì số sản phẩm làm được là (45+9).8=432 sản phẩm.

1:
Giải:
Phân số chỉ 1 giờ bác Thành làm được là:
\(1:3=\frac{1}{3}\) ( công việc )
Phân số chỉ 1 giờ bác Mai làm được là:
\(1:4=\frac{1}{4}\) ( công việc)
Phân số chỉ 1 giờ cả hai bác làm được là:
\(\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\) ( công việc )
Nếu hai bác cùng làm thì sau số giờ xong công việc là:
\(1:\frac{7}{12}=\frac{12}{7}\) ( giờ )
Vậy nếu cả hai bác cùng làm thì sau \(\frac{12}{7}\) giờ sẽ xong công việc
2:
Giải:
Phân số chỉ 2 giờ người thứ nhất đi được là:
\(2:3=\frac{2}{3}\) ( quãng đường AB )
Phân số chỉ 2 giờ người thứ hai đi được là:
\(2:4=\frac{2}{4}=\frac{1}{2}\) ( quãng đường AB )
Phân số chỉ 5 km là:
\(\frac{2}{3}-\frac{1}{2}=\frac{1}{6}\) ( quãng đường AB )
Quãng đường AB dài là:
\(5:\frac{1}{6}=30\) ( km )
Vậy quãng đường AB dài 30km

Gọi x (ngày) là số ngày dự định làm xong kế hoạch (x > 0).
Khi đó:
Số sản phẩm dự định làm trong một ngày là: 360/x (sản phẩm)
Thực tế, mỗi ngày làm thêm được 9 sản phẩm nên năng suất thực tế là: 360/x + 9 (sản phẩm / ngày)
Số ngày làm thực tế là: x – 1 (ngày)
Số sản phẩm làm được trong x – 1 ngày là: 360 + 360.5% = 378 sản phẩm.
Ta có phương trình:
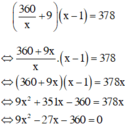
⇔ x = 8 (thỏa mãn) hoặc x = –5 (loại)
Số ngày dự định là 8 ngày, năng suất thực tế là 360:8 + 9 = 54 sản phẩm/ngày
Vậy khi đến hạn, phân xưởng sẽ làm được 54.8 = 432 sản phẩm.

Bài này qúa dễ đối vói mk
Giả sử 1 ngày làm hết công việc đó thì cần số người là :
60 x 24 = 1440 ( người )
Nếu 18 ngày làm hết công việc đó cần số người là :
1440 : 18 = 80 ( người )
Số người đến thêm là :
80 - 60 = 20 ( người )
Đáp số : 20 người
Coi 1 công nhân làm một ngày được một công.
Như vậy tổng số công là:
1 x 60 x 24 =1440 (công )
Do số công nhân đến thêm nên mỗi ngày làm được số công là:
1440 : 18 = 80 (công)
Do đó số công nhân là:
80 : 1 = 80 (người)
Số công nhân đến thêm là;
80 - 60 =20 (người)