Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi vật qua VTCB thì vận tốc đạt cực đại
\(\Rightarrow v_{max}=\omega.A=\sqrt{\dfrac{g}{l}}.\alpha_0.l=\sqrt{g.l}\alpha_0\)
\(\Rightarrow l=\dfrac{v_{max}^2}{g.\alpha_0^2}=25000(cm)=250m\)

bạn để ý có công thức T= \(mg\left(3cos\alpha-2cos\alpha_0\right)\)
còn P= mg
vậy T/P= \(3cos\alpha-2cos\alpha_0\)
a0* l = S0 bạn suy ra a0 ( l: chiều dài con lắc ; w2 = g/l)
chú ý: con lắc qua vị trí cân bằng tức \(\alpha=0\) suy ra cos \(\alpha\) = 1
suy ra T/P cần tìm = 3 - 2cos\(\alpha_0\)
bạn hiểu rồi thì tính nốt nhé

- Vận tốc ở vị trí thấp nhất là vận tốc cực đại:
\(v_{max}=\omega.A=\sqrt{\dfrac{g}{l}}.\alpha.l=\sqrt{gl}\alpha\)
- Gia tốc ở vị trí cao nhất (ở biên)
\(a_{max}=\omega^2.A=\dfrac{g}{l}.\alpha.l=g.\alpha\)
\(\Rightarrow \alpha=\dfrac{a_{max}}{g}=1/10(rad)\)
\(\Rightarrow \alpha=5,73^0\)
P.S: Không cần dùng đến giả thiết vận tốc ở vị trí thấp nhất.

Hệ số hồi phục: \(k=\frac{mg}{l}\)
Lực kéo về: \(F=k.x=\frac{mg}{l}.\alpha.l=mg.\alpha\)
Góc lệch: \(\alpha=\frac{\alpha_0}{2}=\frac{0,1}{2}=0,05rad\)
\(\Rightarrow F=0,1.10.0,05=0,05N\)
Độ lớn của lực kéo về:\(F = ks\), \(s\) là li độ cong của con lắc đơn.
Vật ở vị trí có li độ cong bằng lửa biên độ tức
\(F = k \frac{S_0}{2}= \frac{k.\alpha_0.l}{2}\) (do \(s_0 = \alpha_0 .l\))
\(=m\omega ^2.\frac{\alpha_0.l}{2}=\frac{mg\alpha_0}{2}=\frac{0,1.10.0,1}{2}=5.10^{-2}N.\)
Vậy lức kéo về tại vị trí đó là \(F = 5.10^{-2}N.\)

Đáp án A
Phương pháp: Sử dụng lí thuyết về gia tốc trong dao động của con lắc đơn
Cách giải:
- Gia tốc của vật tại VTCB
+ Gia tốc tiếp tuyến:
![]()
+ Gia tốc hướng tâm:
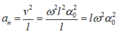
=> Gia tốc tại VTCB là:
![]()
- Gia tốc tại VT biên
+ Gia tốc tiếp tuyến:

+ Gia tốc hướng tâm:
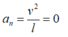
=> Gia tốc tại VT biên là:
![]()
Từ (1) và (2)
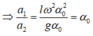
Chọn A