Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn đổi ra cùng hàm cos rồi lấy máy tính mà bấm cho nhanh :)

Tại những điểm cách O một đoạn x thì biên độ giảm \(2.5\sqrt{x}\)lần
=> biên độ tại điểm M cách O một đoạn 25cm là \(\frac{2}{2,5.\sqrt{25}} = 0.16cm. \)
M trễ pha hơn O:
\(u_M=0.16\cos(4\pi t - 2\pi\frac{OM}{\lambda})= 0.16\cos(40\pi t - \frac{5\pi}{3})cm.\)

Theo bài ra ta có 2= A.\(\omega^2\) => A = \(\frac{2}{\omega^2}=\frac{2}{\left(\frac{1}{2}\right)^2}=8\left(cm\right)\)
T = 4\(\pi\left(s\right)\)
ta suy ra phương trình li độ của vật : x=\(8\) .cos (\(\frac{t}{2}+\frac{\pi}{2}\) )
1 chu kì thì vật sẽ đi qua vị trí x=\(4\sqrt{3}\) 2 lần
lần thứ 3 qua vị trí thì vật đã quay được một chu kì và góc \(\varphi=\) \(\frac{4\pi}{3}\)
Tổng thời gian : t = T + 2T/3 = 5T/3 = \(\frac{20\pi}{3}\left(s\right)\)

Biên độ dao động tổng hợp thỏa mãn: \(\left|A_1-A_2\right|\le A\le\left|A_1+A_2\right|\)
\(\Rightarrow\) A = 5 (cm) thỏa mãn hệ thức

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)
+ \(\omega = 2\pi f = 2\pi .10 = 20\pi \ (rad/s) \)
+ A = 4cm.
+ t = 0, vật qua x0 = A \(\Rightarrow\left\{ \begin{array}{} x_0 = 4\ cm\\ v_0 =0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 1\ cm\\ \sin \varphi = 0 \end{array} \right. \Rightarrow \varphi = 0\)
Vậy phương trình dao động: \(x = 4\cos(20\pi t) \ (cm)\)

 D
D
Đáp án B
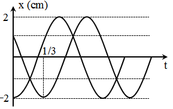
Dễ dàng có được w = 2p rad/s Þ T = 1 s Þ 1/3 = T/3.
Phương trình dao động 1 (li độ x = -2 cm tại t = 0) là: x = -2cos(2pt + p) cm.
Sau khoảng thời gian T/3 thì dao động 2 về đến biên âm Þ tại t = 0, li độ x2 = 1 cm.
Suy ra phương trình x2 = 2cos(2pt + p/3) Þ x = x1 + x2 = 2cos(2pt + 2p/3) cm là phương trình tổng hợp.