em bài này với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AN
1
2
22 tháng 5 2023
Ptr có `2` nghiệm phân biệt `<=>\Delta' > 0`
`=>(m+1)^2-m^2+2m-3 > 0`
`<=>m^2+2m+1-m^2+2m-3 > 0`
`<=>m > 1/2`
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=2m+2),(x_1.x_2=c/a=m^2-2m+3):}`
Ta có: `1/[x_1 ^2]-[4x_2]/[x_1]+3x_2 ^2=0`
`=>1-4x_1.x_2+3(x_1.x_2)^2=0`
`<=>1-4(m^2-2m+3)+3(m^2-2m+3)^2=0`
`<=>[(m^2-2m+3=1),(m^2-2m+3=1/3):}`
`<=>[(m^2-2m+2=0(VN)),(m^2-2m+8/3=0(VN)):}`
`=>` Không có `m` thỏa mãn.
5 tháng 9 2021
a: ĐKXĐ: \(x\in R\)
b: ĐKXĐ: \(x\ne\dfrac{1}{2}\)
c: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\x\ne\dfrac{1}{2}\end{matrix}\right.\)
d: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\)
HK
1
10 tháng 7 2023
Gọi vận tốc của ô tô là x
=>Vận tốc xe máy là x-10
Theo đề, ta có: 120/(x-10)-120/x=1
=>(120x-120x+1200)/x(x-10)=1
=>x^2-10x=1200
=>x^2-10x-1200=0
=>x=40
29 tháng 6 2021
Bài 7:
Ta có: \(C=\dfrac{4+\sqrt{7}}{3\sqrt{2}+\sqrt{4+\sqrt{7}}}+\dfrac{4-\sqrt{7}}{3\sqrt{2}-\sqrt{4-\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{6+\sqrt{8+2\sqrt{7}}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{6-\sqrt{8-2\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{7+\sqrt{7}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{7-\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(\sqrt{7}-1\right)\left(4+\sqrt{7}\right)}{6\sqrt{7}}+\dfrac{\sqrt{2}\left(\sqrt{7}+1\right)\left(4-\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(-3+3\sqrt{7}+3+3\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\sqrt{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 6 2021
6.
Ta có:
\(A=\sqrt{20+\sqrt{20+...+\sqrt{20}}}>\sqrt{20+\sqrt{\dfrac{1}{16}}}=\dfrac{9}{2}\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}>\sqrt[3]{24}=\sqrt[3]{\dfrac{192}{8}}>\sqrt[3]{\dfrac{125}{8}}=\dfrac{5}{2}\)
\(\Rightarrow A+B>\dfrac{9}{2}+\dfrac{5}{2}=7\)
\(A=\sqrt[]{20+\sqrt[]{20+...+\sqrt[]{20}}}< \sqrt[]{20+\sqrt[]{20+...+\sqrt[]{25}}}=5\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}< \sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{27}}}=3\)
\(\Rightarrow A+B< 5+3=8\)
20 tháng 8 2021
Bạn làm thiếu rồi nhé. Đoạn này lúc đầu mình cũng phân vân nhưng vẫn tính được x và y
HP
20 tháng 8 2021
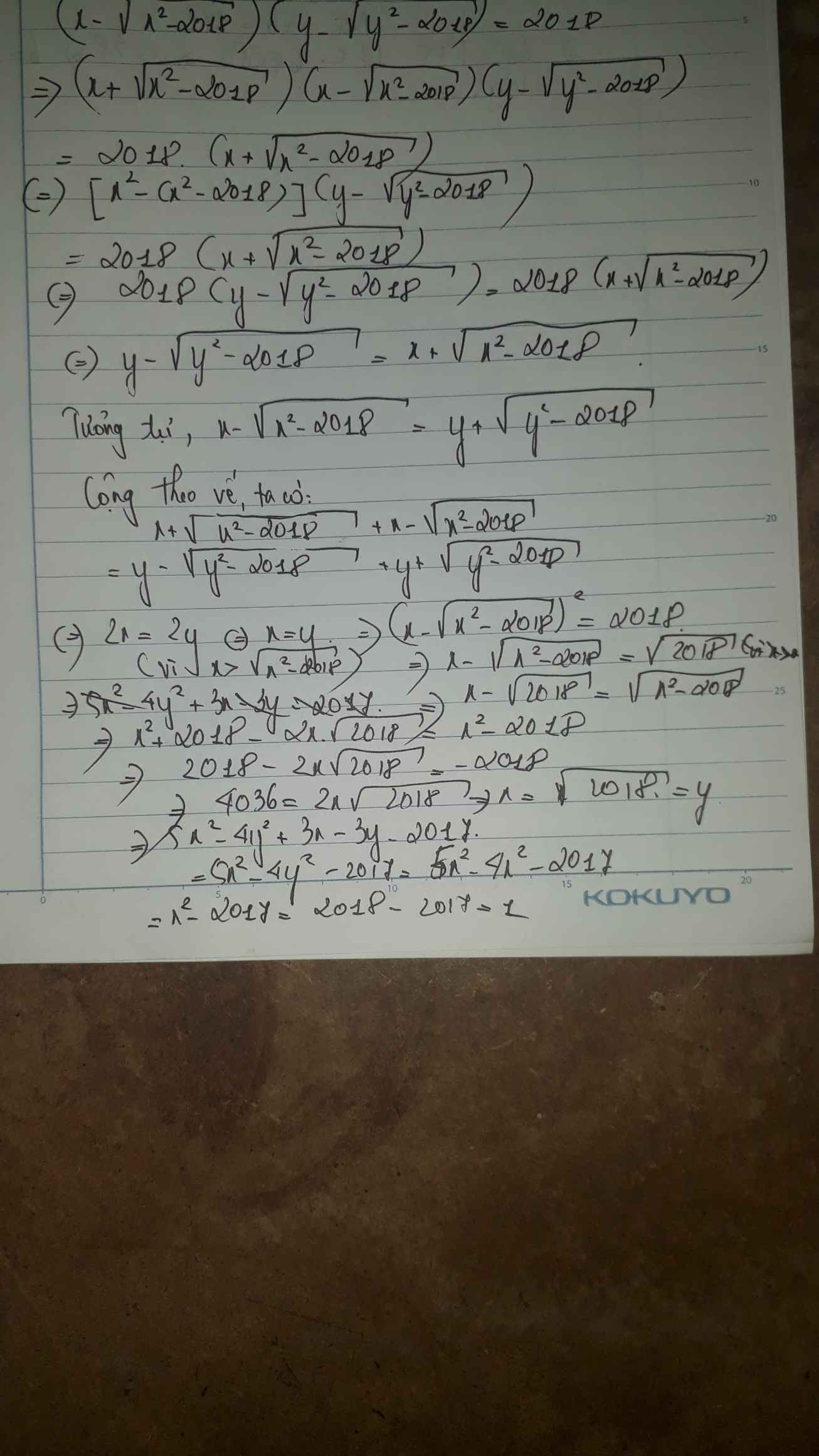
1.
ĐK: \(x,y\ge\sqrt{2018};x,y\le-\sqrt{2018}\)
\(\left(x-\sqrt{x^2-2018}\right)\left(y^2-2018\right)=2018\left(1\right)\)
\(\Leftrightarrow\left(x-\sqrt{x^2-2018}\right)\left(y-\sqrt{y^2-2018}\right)=2018\)
\(\Leftrightarrow2018\left(y-\sqrt{y^2-2018}\right)=2018\left(x+\sqrt{x^2-2018}\right)\)
\(\Leftrightarrow y-\sqrt{y^2-2018}=x+\sqrt{x^2-2018}\left(2\right)\)
Mặt khác:
\(\left(1\right)\Leftrightarrow2018\left(x-\sqrt{x^2-2018}\right)=2018\left(y+\sqrt{y^2-2018}\right)\)
\(\Leftrightarrow x-\sqrt{x^2-2018}=y+\sqrt{y^2-2018}\left(3\right)\)
Trừ vế theo vế (2) cho (3):
\(y-\sqrt{y^2-2018}-x+\sqrt{x^2-2018}=x+\sqrt{x^2-2018}-y-\sqrt{x^2-2018}\)
\(\Leftrightarrow x=y\)
Khi đó:
\(5x^2-4y^2+3x-3y-2017=x^2-2017\)
HK
3
HP
6 tháng 2 2022
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}+\dfrac{1}{2-\sqrt{x}}\left(đk:x\ge0;x\ne4\right)\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-2}\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{3+2\sqrt{x}-4-\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{1}{\sqrt{x}+1}\)
HP
6 tháng 2 2022
\(S=\left(\dfrac{1}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}-2}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\left(đk:x\ge0;x\ne1\right)\)
\(S=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\)
\(S=\dfrac{\sqrt{x}-2+x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{x+4\sqrt{x}+4}{1-\sqrt{x}}\)
\(S=\dfrac{x+3\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}\)
\(S=\dfrac{\left(x+3\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\left(1-\sqrt{x}\right)}\)
(đến đoạn này thì trong ngoặc ko tách ra đc nữa nên mik nghĩ là đến đây là xong, nếu sai thì bn nói mik)
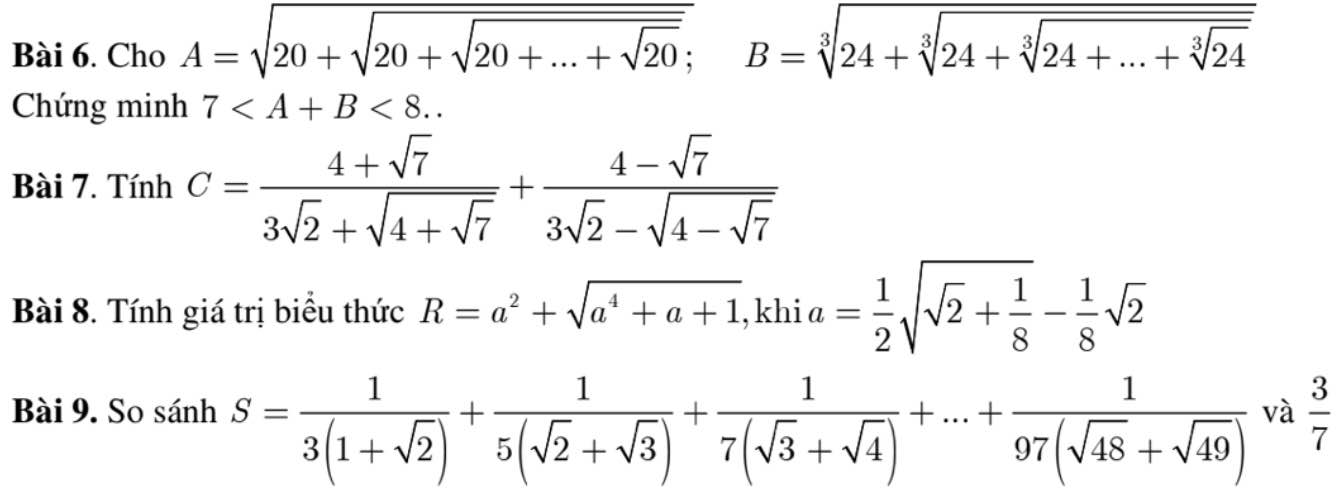
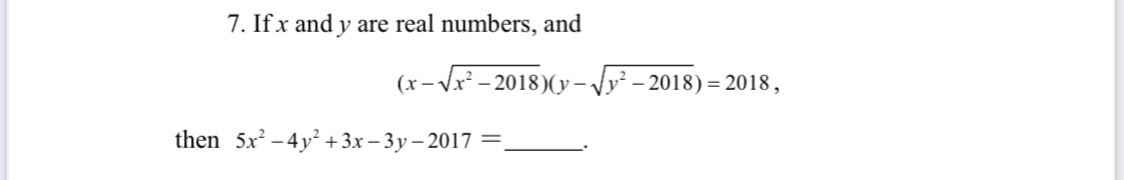
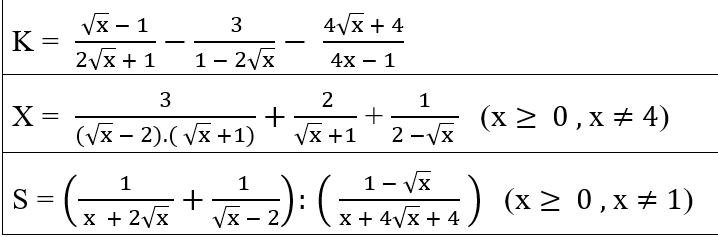
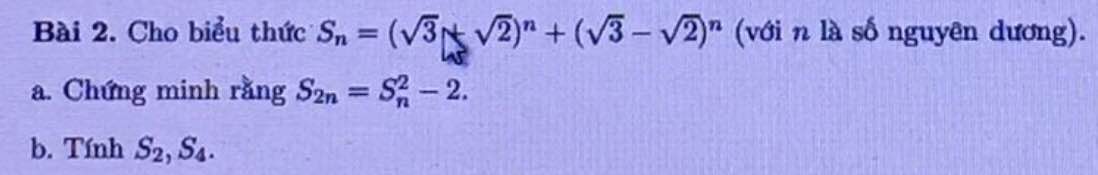mọi người giải giúp em bài này với ạ 🥺
are you about that ?
EM ĐANg cần gấp bài 1 ạ