Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Con a) Đang nghĩ
b) D = d2 + 10e2 - 6de - 10e + 26
D= d2 - 2.3de + ( 3e)2 + e2 - 2.5e + 52 + 1
D= ( d - 3e)2 + ( e - 5)2 + 1
Do : ( d - 3e)2 lớn hơn hoặc bằng 0 với moi d, e
( e - 5)2 lớn hơn hoặc bằng 0 với mọi e
Vậy : ( d - 3e)2 + 1 lớn hơn hoặc bằng 1 với moi d, e
( e - 5)2 + 1 lớn hơn hoặc bằng 1 với mọi e
Vậy Dmin = 1 khi e = 5 . d = 15
c) E = 4x2 + 12x + 11
E = ( 2x)2 + 2.2x.3 + 32 + 2
E= ( 2x + 3)2 + 2
Do : ( 2x + 3)2 lớn hơn hặc bằng 0 với mọi x
--> ( 2x + 3)2 + 2 lớn hơn hặc bằng 2 với mọi x
Vậy , Emin = 2 KHI VÀ CHỈ KHI \(\dfrac{-3}{2}\)
A = 4x4 + 12x2 + 11
A = ( 2x2)2 + 2.2x2.3 + 32 + 2
A = ( 2x + 3)2 + 2
Do : ( 2x + 3)2 lớn hơn hoặc bằng 0 với mọi x
Suy ra : ( 2x + 3)2 + 2 lớn hơn hoặc bằng 2 với mọi x
Vậy , Amin = 2 khi và chỉ khi : 2x + 3 = 0 -> x = \(-\dfrac{3}{2}\)

1. a. \(A=8a-8a^2+3=-8\left(a-\frac{1}{2}\right)^2+5\)
Vì \(\left(a-\frac{1}{2}\right)^2\ge0\forall a\)\(\Rightarrow-8\left(a-\frac{1}{2}\right)^2+5\le5\)
Dấu "=" xảy ra \(\Leftrightarrow-8\left(a-\frac{1}{2}\right)^2=0\Leftrightarrow a-\frac{1}{2}=0\Leftrightarrow a=\frac{1}{2}\)
Vậy Amax = 5 <=> a = 1/2
b. \(B=b-\frac{9b^2}{25}=-\frac{9}{25}\left(b-\frac{25}{18}\right)^2+\frac{25}{36}\)
Vì \(\left(b-\frac{25}{18}\right)^2\ge0\forall b\)\(\Rightarrow-\frac{9}{25}\left(b-\frac{25}{18}\right)^2+\frac{25}{36}\le\frac{25}{36}\)
Dấu "=" xảy ra \(\Leftrightarrow-\frac{9}{25}\left(b-\frac{25}{18}\right)^2=0\Leftrightarrow b-\frac{25}{18}=0\Leftrightarrow b=\frac{25}{18}\)
Vậy Bmax = 25/36 <=> b = 25/18
a,\(A=8a-8a^2+3\)
\(=-8\left(a^2-a\right)+3\)
\(=-8\left(a^2-2a\frac{1}{2}+\frac{1}{4}-\frac{1}{4}\right)+3\)
\(=-8\left[\left(a-\frac{1}{2}\right)^2-\frac{1}{4}\right]+3\)
\(=-8\left(a-\frac{1}{2}\right)^2+2+3\)
\(=-8\left(a-\frac{1}{2}\right)^2+5\le5\forall a\)
Dấu"=" xảy ra khi \(\left(a-\frac{1}{2}\right)^2=0\Rightarrow a=\frac{1}{2}\)
Vậy \(Max_A=5\)khi\(a=\frac{1}{2}\)
bài 2:
b,\(D=d^2+10e^2-6de-10e+26\)
\(=d^2-23de+\left(3e\right)^2+e^2-2.5e+5^2+1\)
\(=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\forall d,e\)
Dấu"=" xảy ra khi\(\orbr{\begin{cases}\left(d-3e\right)^2=0\\\left(e-5\right)^2=0\end{cases}\Rightarrow\orbr{\begin{cases}d=15\\e=5\end{cases}}}\)
vậy \(D_{min}=1\)khi \(d=15;e=5\)
c,:\(E=4x^4+12x^2+11\)
\(=\left(2x^2\right)^2+2.2x^2.3+3^2+2\)
\(=\left(2x^2+3\right)^2+2\ge2\forall x\)
còn 1 đoạn nx bạn tự lm tiếp,lm giống như D

a) A = x2 + 12x + 39
= ( x2 + 12x + 36 ) + 3
= ( x + 6 )2 + 3 ≥ 3 ∀ x
Đẳng thức xảy ra ⇔ x + 6 = 0 => x = -6
=> MinA = 3 ⇔ x = -6
B = 9x2 - 12x
= 9( x2 - 4/3x + 4/9 ) - 4
= 9( x - 2/3 )2 - 4 ≥ -4 ∀ x
Đẳng thức xảy ra ⇔ x - 2/3 = 0 => x = 2/3
=> MinB = -4 ⇔ x = 2/3
b) C = 4x - x2 + 1
= -( x2 - 4x + 4 ) + 5
= -( x - 2 )2 + 5 ≤ 5 ∀ x
Đẳng thức xảy ra ⇔ x - 2 = 0 => x = 2
=> MaxC = 5 ⇔ x = 2
D = -4x2 + 4x - 3
= -( 4x2 - 4x + 1 ) - 2
= -( 2x - 1 )2 - 2 ≤ -2 ∀ x
Đẳng thức xảy ra ⇔ 2x - 1 = 0 => x = 1/2
=> MaxD = -2 ⇔ x = 1/2
Ta có A = x2 + 12x + 39 = (x2 + 12x + 36) + 3 = (x + 6)2 + 3 \(\ge\)3
Dấu "=" xảy ra <=> x + 6 = 0
=> x = -6
Vậy Min A = 3 <=> x = -6
Ta có B = 9x2 - 12x = [(3x)2 - 12x + 4] - 4 =(3x - 2)2 - 4 \(\ge\)-4
Dấu "=" xảy ra <=> 3x - 2 =0
=> x = 2/3
Vậy Min B = -4 <=> x = 2/3
b) Ta có C = 4x - x2 + 1 = -(x2 - 4x - 1) = -(x2 - 4x + 4) + 5 = -(x - 2)2 + 5 \(\le\)5
Dấu "=" xảy ra <=> x - 2 = 0
=> x = 2
Vậy Max C = 5 <=> x = 2
Ta có D = -4x2 + 4x - 3 = -(4x2 - 4x + 1) - 2 = -(2x - 1)2 - 2 \(\le\)-2
Dấu "=" xảy ra <=> 2x - 1 = 0
=> x = 0,5
Vậy Max D = -2 <=> x = 0,5

Câu hỏi của ĐỖ THỊ HƯƠNG TRÀ - Toán lớp 8 - Học trực tuyến OLM
mình làm rồi nhé, bạn kham khảo link

\(A=\frac{1}{16}c^2-9c+10\)
\(A=\left(\frac{1}{16}c^2-9c+324\right)-314\)
\(A=\left(\frac{1}{4}c-18\right)^2-314\)
Mà \(\left(\frac{1}{4}c-18\right)^2\ge0\forall c\)
\(\Rightarrow A\ge-314\)
Dấu "=" xảy ra khi : \(\frac{1}{4}c-18=0\Leftrightarrow c=72\)
Vậy ...
\(B=d^2+10e^2-6de-10e+26\)
\(B=\left(d^2-6de+9e^2\right)+\left(e^2-10e+25\right)+1\)
\(B=\left(d-3e\right)^2+\left(e-5\right)^2+1\)
Mà \(\left(d-3e\right)^2\ge0\forall d;e\)
\(\left(e-5\right)^2\ge0\forall e\)
\(\Rightarrow B\ge1\)
Dấu "=" xảy ra khi : \(\hept{\begin{cases}d-3e=0\\e-5=0\end{cases}}\Leftrightarrow\hept{\begin{cases}d=15\\e=5\end{cases}}\)
Vậy ...
a, \(A=\frac{1}{16}c^2-9c+10=\left(\frac{1}{16}c^2-9c+324\right)-314=\left(\frac{1}{4}c-18\right)^2-314\ge-314\)
Dấu "=" xảy ra khi \(\frac{1}{4}c-18=0\Leftrightarrow c=72\)
Vậy Amin = -314 khi c = 72
b, \(B=d^2+10e^2-6de-10e+26\)
\(=\left(d^2-6de+9e^2\right)+\left(e^2-10e+25\right)+1\)
\(=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}d-3e=0\\e-5=0\end{cases}\Leftrightarrow\hept{\begin{cases}d-15=0\\e=5\end{cases}\Leftrightarrow}\hept{\begin{cases}d=15\\e=5\end{cases}}}\)
Vậy Bmin = 1 khi d = 15, e = 5

Ta có : A = x2 - 4x + 1
=> A = x2 - 2.x.2 + 4 - 3
=> A = (x - 2)2 - 3
Mà : (x - 2)2 \(\ge0\forall x\in R\)
Nên : (x - 2)2 - 3 \(\ge-3\forall x\in R\)
Vậy GTNN của A là -3 khi x = 2
\(B=4x^2+4x+11=\left(2x\right)^2+2.2x.1+1+10=\left(2x+1\right)^2+10\)
Vì \(\left(2x+1\right)^2\ge0\Rightarrow B=\left(2x+1\right)^2+10\ge10\)
Dấu "=" xảy ra khi (2x+1)2=0 <=> 2x+1=0 <=> x=-1/2
Vậy gtnn của B là 10 khi x=-1/2
---
\(C=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)=\left(x^2+5x-6\right)\left(x^2+5x+6\right)=\left(x^2+5x\right)^2-36\ge-36\)
Dấu "=" xảy ra khi x=0 hoặc x=-5
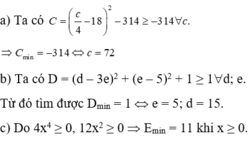
\(A=\dfrac{1}{16}c^2-9c+10=\dfrac{1}{16}\left(x-72\right)^2-314\ge-314\)
\(A_{min}=-314\) khi \(c=72\)
\(B=\left(d^2-6de+9e^2\right)+\left(e^2-10e+25\right)+1=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\)
\(B_{min}=1\) khi \(\left\{{}\begin{matrix}d=15\\e=5\end{matrix}\right.\)
\(C=4x^4+12x^2+11\)
Do \(\left\{{}\begin{matrix}x^4\ge0\\x^2\ge0\end{matrix}\right.\) ; \(\forall x\Rightarrow C\ge11\)
\(C_{min}=11\) khi \(x=0\)
a) Ta có: \(\dfrac{1}{16}c^2-9c+10\)
\(=\left(\dfrac{1}{4}c\right)^2-2\cdot\dfrac{1}{4}c\cdot18+324-314\)
\(=\left(\dfrac{1}{4}c-18\right)^2-314\ge-314\forall c\)
Dấu '=' xảy ra khi \(\dfrac{1}{4}c=18\)
hay c=72
Vậy: Giá trị nhỏ nhất của biểu thức \(\dfrac{1}{16}c^2-9c+10\) là -314 khi c=72
b) Ta có: \(d^2+10e^2-6de-10e+26\)
\(=d^2-6de+9e^2+e^2-10e+25+1\)
\(=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\forall d,e\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}e=5\\d=3e=3\cdot5=15\end{matrix}\right.\)
Vậy: Giá trị nhỏ nhất của biểu thức \(d^2+10e^2-6de-10e+26\) là 1 khi e=5 và d=15
c) Ta có: \(4x^4+12x^2+11\)
\(=4x^4+12x^2+9+2\)
\(=\left(2x^2+3\right)^2+2\ge3^2+2=11\)
Dấu '=' xảy ra khi x=0
Vậy: Giá trị nhỏ nhất của biểu thức \(4x^4+12x^2+11\) là 11 khi x=0