NN
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 11 2021
Câu 2:
\(\Leftrightarrow\left(x+2\right)\left(10x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-\dfrac{3}{10}\end{matrix}\right.\)
31 tháng 10 2021
\(a,\Leftrightarrow x^2-x+2021x-2021=0\\ \Leftrightarrow\left(x-1\right)\left(x+2021\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2021\end{matrix}\right.\\ b,\Leftrightarrow-5x^2+15x+x-3=0\\ \Leftrightarrow\left(x-3\right)\left(1-5x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)
31 tháng 10 2021
b: \(-5x^2+16x-3=0\)
\(\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)
3 tháng 5 2022
Câu 9:
a. <=> 4x= 12
<=> x=3
S={3}
b. <=> (2x-6).(x+9)=0
<=> 2x-6=0 hoặc x+9=0
<=> x= 3 hoặc x=-9
S={3;-9}
c. <=> 5x=-20
<=> x= -4
S={-4}
d. <=> (2x-6).(3x+9)=0
<=> 2x-6=0 hoặc 3x+9=0
<=> 2x=6 hoặc 3x=-9
<=> x=3 hoặc x= -3
S={3;-3}
e. th1: 2x-3= 6x+5 nếu 2x-3>0 => x>\(\dfrac{3}{2}\)
2x-3=6x+5
<=>2x-6x= 5+3
<=>-4x=8
<=> x= -2 (loại)
th2: 2x-3= -6x+5 nếu 2x-3<0 => x<\(\dfrac{3}{2}\)
2x-3=-6x+5
<=>2x+6x= 5+3
<=>8x=8
<=>x=1 (chọn)
S={1}
f. <=> -12x>6
<=> x< -\(\dfrac{1}{2}\)
S={x/x<-\(\dfrac{1}{2}\)}
g. th1: 2x+3=4x+5 nếu 2x+3>0 => x>\(\dfrac{-3}{2}\)
2x+3=4x+5
2x-4x=5-3
-2x= 2
x= -1 (chọn)
th2: 2x+3=-4x+5 nếu 2x+3<0 => x<\(\dfrac{-3}{2}\)
2x+3=-4x+5
2x+4x= 5-3
6x=2
x= \(\dfrac{1}{3}\)(loại)
S={-1}
h. <=> -2x>-6
<=> x< 3
S={x/x<3}
NT
1
A
0
LP
19 tháng 8 2021
3x.(x-2)-x2+2x=0
⇔3x2-6x-x2+2x=0
⇔2x2-4x=0
⇔2x(x-2)=0
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
vậy x=0 và x=2
19 tháng 8 2021
3x(x-2)-x^2+2x=0
<=>3x(x-2)-x(x-2)=0
<=>(3x-x)(x-2)=0
<=>2x(x-2)=0
<=>2x=0 hoặc x-2=0
<=>x=0 hoặc x=2
21 tháng 8 2017
\(x^4-10x^3+35x^2+24>0\)
\(\Leftrightarrow x^4-2.5.x^3+\left(5x\right)^2+10x^2+24>0\)
\(\Leftrightarrow\left(x^2-5x\right)^2+10x^2+24>0\)
\(\Leftrightarrow x^2\left(x-5\right)^2+10x^2+24>0\)(luôn đúng)
Vậy nghiệm của bất phương trình \(x\in R\)
NT
3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 12 2023
câu a, \(\dfrac{x}{x+1}\); \(\dfrac{x^2}{1-x}\); \(\dfrac{1}{x^2-1}\) (đk \(x\)≠ -1; 1)
\(x^2\) - 1 = ( \(x\) - 1).(\(x\) + 1)
\(\dfrac{x}{x+1}\) = \(\dfrac{x.\left(x-1\right)}{\left(x+1\right).\left(x-1\right)}\);
\(\dfrac{x^2}{1-x}\) = \(\dfrac{-x^2}{x-1}\)= \(\dfrac{-x^2.\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{1}{x^2-1}\) = \(\dfrac{1}{\left(x-1\right)\left(x+1\right)}\)
b, \(\dfrac{10}{x+2}\); \(\dfrac{5}{2x-4}\); \(\dfrac{1}{6-3x}\) (đk \(x\) ≠ -2; 2)
2\(x-4\) = 2.(\(x\) - 2); 6 - 3\(x\) = - 3.(\(x\) - 2)
\(\dfrac{10}{x+2}\) = \(\dfrac{10.2.3\left(x-2\right)}{2.3\left(x+2\right)\left(x-2\right)}\) = \(\dfrac{60\left(x-2\right)}{6\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{5}{2x-4}\) = \(\dfrac{5.3\left(x+2\right)}{2.3\left(x-2\right).\left(x+2\right)}\) = \(\dfrac{15.\left(x+2\right)}{6.\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{1}{6-3x}\) = \(\dfrac{-1}{3.\left(x-2\right)}\) = \(\dfrac{-1.\left(x+2\right)}{3.2.\left(x-2\right)\left(x+2\right)}\) = \(\dfrac{-2.\left(x+2\right)}{6.\left(x-2\right).\left(x+2\right)}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 12 2023
c, \(\dfrac{x}{2x-4}\); \(\dfrac{1}{2x+4}\) và \(\dfrac{3}{4-x^2}\) đk \(x\) ≠ 2; -2
\(\dfrac{x}{2x-4}\) = \(\dfrac{x}{2.\left(x-2\right)}\) = \(\dfrac{x.\left(x+2\right)}{2.\left(x-2\right).\left(x+2\right)}\)
\(\dfrac{1}{2x+4}\) = \(\dfrac{1}{2.\left(x+2\right)}\) = \(\dfrac{\left(x-2\right)}{2.\left(x+2\right).\left(x-2\right)}\)
\(\dfrac{3}{4-x^2}\) = \(\dfrac{-3}{\left(x-2\right)\left(x+2\right)}\) = \(\dfrac{-6}{2.\left(x-2\right)\left(x+2\right)}\)
KT
16 tháng 3 2018
\(\Delta SAB\) có \(CF//AB\), áp dụng hệ quả định lý Talet ta có:
\(\frac{SA}{SC}=\frac{SB}{SF}\) (1)
\(\Delta SBC\)có \(EF//CB\), áp dụng hệ quả định lý Talet ta có:
\(\frac{SC}{SE}=\frac{SB}{SF}\) (2)
Từ (1) và (2) suy ra: \(\frac{SA}{SC}=\frac{SC}{SE}\)
\(\Rightarrow\)\(SC^2=SE.SA\)
P/s: mk ko bt đúng or sai, bn đọc tham khảo.
mk sai đâu thì chỉ hộ mk nha
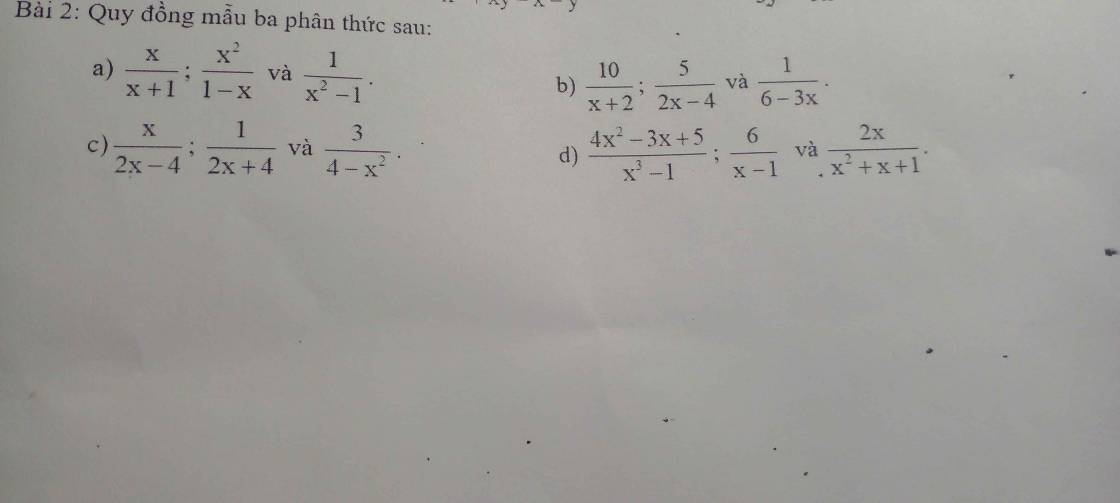
c)\(x^2y-xy^2-3x+3y=xy\left(x-y\right)-3\left(x-y\right)=\left(xy-3\right)\left(x-y\right)\)
d)\(x\left(x+y\right)^2-y\left(x+y\right)^2+xy-x^2\)
\(=\left(x+y\right)^2\left(x-y\right)+x\left(y-x\right)\)
\(=\left(x-y\right)\left[\left(x+y\right)^2+x\right]=\left(x-y\right)\left(x^2+2xy+y^2+x\right)=x\left(x-y\right)\left(x+2y+1\right)\)
e)\(3a^2x-3a^2y+abx-aby=3a^2\left(x-y\right)+ab\left(x-y\right)=\left(3a^2+ab\right)\left(x-y\right)\)
\(=a\left(3a+b\right)\left(x-y\right)\)
Trả lời:
c, x2y - xy2 - 3x + 3y
= ( x2y - 3x ) - ( xy2 - 3y )
= x ( xy - 3 ) - y ( xy - 3 )
= ( x - y ) ( xy - 3 )
d, x ( x + y )2 - y ( x + y )2 + xy - x2
= ( x + y )2 ( x - y ) - ( x2 - xy )
= ( x + y )2 ( x - y ) - x ( x - y )
= ( x - y ) [ ( x + y )2 - x ]
= ( x - y ) ( x2 + 2xy + y2 - x )
e, 3a2x - 3a2y + abx - aby
= ( 3a2x - 3a2y ) + ( abx - aby )
= 3a2 ( x - y ) + ab ( x - y )
= ( 3a2 + ab ) ( x - y )
= a ( 3a + b ) ( x - y )