
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu b đề bài thiếu, tìm giao tuyến của mặt nào và (ABD) vậy em?

\(A^3_n+5A^2_n=2\left(n+15\right)\)
ĐK: n ≥ 3 (n∈N)
<=> \(\dfrac{n!}{\left(n-3\right)!}+\dfrac{5.n!}{\left(n-2\right)!}=2\left(n+15\right)\)
<=> \(\dfrac{n\left(n-1\right)\left(n-2\right)\left(n-3\right)!}{\left(n-3\right)!}+\dfrac{5n\left(n-1\right)\left(n-2\right)!}{\left(n-2\right)!}=2\left(n+15\right)\)
<=> \(n\left(n-1\right)\left(n-2\right)+5\left(n-1\right)n-2n-30=0\)
<=> \(n^3+2n^2-5n-30=0\) <=> n=3

Đáp án C.
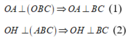
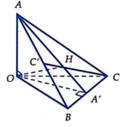
Từ (1) và (2) suy ra
![]()
=> AH là đường cao trong tam giác BCD
Tương tự suy ra, CH là đường cao trong tam giác BCD => H là trực tâm => I đúng => II sai
+ Gọi ![]()
=> 1 O H 2 = 1 O B 2 + 1 O C 2 => 1 O H 2 = 1 O A ' 2 + 1 O A 2 = 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
=> III đúng

Do \(SO\perp ABC\Rightarrow\) các tam giác SOA, SOB, SOC đều vuông tại O
Đặt \(SA=SB=SC=a\) , áp dụng Pitago:
\(OA=\sqrt{SA^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OB=\sqrt{SB^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OC=\sqrt{SC^2-SO^2}=\sqrt{a^2-SO^2}\)
\(\Rightarrow OA=OB=OC\Rightarrow O\) là tâm đường tròn ngoại tiếp tam giác ABC

Chọn mp(SMP) có chứa MK
\(O\in MP\subset\left(SMP\right)\)
\(O\in NQ\subset\left(SNQ\right)\)
Do đó: \(O\in\left(SMP\right)\cap\left(SNQ\right)\)
mà \(S\in\left(SMP\right)\cap\left(SNQ\right)\)
nên \(\left(SMP\right)\cap\left(SNQ\right)=SO\)
Gọi giao điểm của SO với MK là A
=>A là giao điểm của MK với mp(SNQ)


bạn lấy hai điểm A,B trên d rồi tính vectơ và độ dài IA,IB. Lấy A',B' là ảnh roòi thực hiện hai phép quay cho pi(rad) sao cho IA=IA' và (IA,IA')=180 độ dựa vào cả hình vẽ nữa thì tìm đk điểm A, tươngtự vs B. mình hướng dẫn vậy thôi A'B' là đt cần tìm