Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lớp có số bạn không thích chơi 2 môn là
\(45-\left(15+12+6\right)=12\) (bạn)
lớp có số bạn không thích chơi 2 môn :
45−(15+12+6)=1245−(15+12+6)=12 (bạn)

Gọi A,B,C là tập hợp các học sinh tích môn toán , Văn , Anh
ta có :
\(\hept{\begin{cases}\left|A\right|=10,\left|B\right|=20,\left|C\right|=25\\\left|A\cap B\cap C\right|=3\\\left|A\cup B\cup C\right|=40\end{cases}}\) ta có : \(\left|A\cup B\cup C\right|=\left|A\right|+\left|B\right|+\left|C\right|-\left(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|\right)+\left|A\cap B\cap C\right|\)
nên \(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|=18\)
Do đó số học sinh chỉ thích đúng hai môn là :
\(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|-3\left|A\cap B\cap C\right|=18-3\times3=9\)

Tham khảo:
Gọi \(x\) là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Ta có: 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông
\( \Rightarrow \) Có \(16 - x\) bạn chỉ tham gia thi đấu bóng đá mà không thi đấu cầu lông.
Và có \(11 - x\) bạn chỉ tham gia thi đấu cầu lông mà không thi đấu bóng đá.
Ta có biểu đồ Ven như sau:
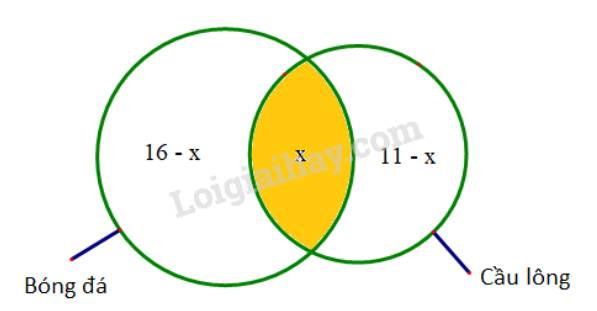
Tổng số bạn tham gia thi đấu bóng đá và cầu lông là: 16-x + x + 11-x = 24 => x=3.
Vậy lớp 10A có 3 bạn tham ggia thi đấu cả bóng đá và cầu lông.

Gọi A, B lần lượt là tập hợp các học sinh thích môn Toán và Tiếng Anh, X là tập hợp học sinh lớp 10H.
Theo giả thiết, \(n(A) = 20,n(B) = 16,n(A \cap B) = 12,n(X) = 35\)

a) Nhận thấy rằng, nếu tính tổng \(n(A) + n(B)\) thì ta được số học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh, nhưng số học sinh thích cả hai môn Toán và Tiếng Anh được tính hai lần. Do đó, số học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh là:
\(n(A \cup B) = n(A) + n(B) - n(A \cap B) = 20 + 16 - 12 = 24\)
b) Trong số 35 học sinh lớp 10H, có 24 học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh, còn lại số học sinh không thích cả hai môn này là: \(35 - 24 = 11\) (học sinh).

Nhân dịp 26/3, trường Cao Nhuyên tổ chức thi đấu các nội dung cờ vua, cờ tướng, bóng bàn. Lớp 10A có 21 học sinh trong đó có 15 bạn tham gia thi đấu cờ vua, 7 bạn tham gia thi đấu cờ tướng và 12 em tham gia thi đấu bóng bàn, ko có em nào đăng kí thi đấu cả 3 nội dung. Biết các bạn có họ lực môn Toán loại yếu kém ko tham gia thi đấu (môn toán dc xếp theo 4 mức: giỏi, khá, trung bình, yếu -kém)... Đọc tiếp
Nhân dịp 26/3, trường Cao Nhuyên tổ chức thi đấu các nội dung cờ vua, cờ tướng, bóng bàn. Lớp 10A có 21 học sinh trong đó có 15 bạn tham gia thi đấu cờ vua, 7 bạn tham gia thi đấu cờ tướng và 12 em tham gia thi đấu bóng bàn, ko có em nào đăng kí thi đấu cả 3 nội dung. Biết các bạn có họ lực môn Toán loại yếu kém ko tham gia thi đấu (môn toán dc xếp theo 4 mức: giỏi, khá, trung bình, yếu -kém) Các bạn được xếp loại giỏi môn toán, nếu dăng kí thì chỉ tham gia thi đúng 1 nội dung. Hỏi có bao nhiêu em đạt loại giỏi về môn toán biết số học sinh xếp loại yếu-kém môn toán là 4 em

Sơ đồ học sinh lớp 10A: 25 bạn 20 bạn 15 bạn 5 1 6 7
Số học sinh thích môn toán và tiếng anh và văn là:(25+15+20)-(5+7+1+6)=42(bạn)
Số học sinh không thích môn nào là:45-42=3(học sinh)
eh8 ihgggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg

Số em không thích Toán là 35-25=10(bạn)
Số em không thích Văn là 35-20=15 bạn
Số em không thích Văn nhưng thích Toán là 15-8=7 bạn
SỐ em không thích Toán nhưng thích Văn là 10-8=2 bạn
SỐ em thích cả Toán và Văn là:
35-8-7-2=35-17=18 bạn
Gọi F, S lần lượt là tập hợp các bạn thích chơi đá bóng, bơi lội.
Dùng công thức \(\left|F\cup S\right|+\left|F\cap S\right|=\left|F\right|+\left|S\right|\)
\(\Rightarrow\left|F\cap S\right|=\left|F\right|+\left|S\right|-\left|F\cup S\right|\) \(=18+15-28=5\)
Vậy có 5 bạn thích cả đá bóng và bơi lội.