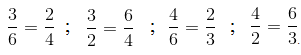Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn ấn vào đúng 0 sẽ ra kết quả, mình làm bài này rồi dễ lắm

Phân tích bài toán:
Trước khi xem đáp số, các bạn để ý rằng: khi ta nhân chéo mỗi cặp phân số bằng nhau trên thì ta đều được đẳng thức 2.3 = 1.6 ban đầu. Chẳng hạn:
2/6 = 1/3 nhân chéo ta được: 2.3 = 1.6;
2/1 = 6/3 nhân chéo ta được: 2.3 = 1.6; ...
Lời giải:
Qua đẳng thức 3.4 = 6.2 lần lượt lấy một thừa số ở vế trái làm tử số còn mẫu số là một thừa số bất kì ở vế phải, chúng ta lập được các cặp phân số bằng nhau sau:
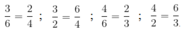

1/
+) \(\frac{3}{6}=\frac{2}{4};\frac{3}{2}=\frac{6}{4};\frac{4}{6}=\frac{2}{3};\frac{4}{2}=\frac{6}{3}\)
2/
\(A=\frac{3n-5}{n+4}=\frac{3n+12-17}{n+4}=\frac{3\left(n+4\right)}{n+4}-\frac{17}{n+4}=3-\frac{17}{n+4}\)
Để A nguyên <=> n + 4 thuộc Ư(17) = {1;-1;17;-17}
| n+4 | 1 | -1 | 17 | -17 |
| n | -3 | -5 | 13 | -21 |
Vậy...
3/
\(S=\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{2016.2017}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2016}-\frac{1}{2017}\)
\(=1-\frac{1}{2017}\)
\(=\frac{2016}{2017}\)
\(A=\frac{3n+12-7}{n+4}=\frac{3\left(n+4\right)}{n+4}-\frac{7}{n+4}=3-\frac{7}{n+4}\)
=> n-4 \(\in\) Ư (7)
n-4=1
n=4+1=5
n-4=-1
n=-1+4=3
n-4=7
n=4+7=11
n-4=-7
n=-7+4=-3

Giải:
Các cặp phân số bằng nhau lập được từ đẳng thưc 3.4 = 6.2 là :
\(\frac{3}{6}=\frac{2}{4}\); \(\frac{6}{2}=\frac{4}{2}\); \(\frac{4}{6}=\frac{2}{3}\); \(\frac{3}{2}=\frac{6}{4}\)
Vậy ...

Lời giải:
$\frac{3}{6}=\frac{2}{4}$
$\frac{6}{3}=\frac{4}{2}$
$\frac{3}{2}=\frac{6}{4}$
$\frac{2}{3}=\frac{4}{6}$

CÁC CẶP PHÂN SỐ BẰNG NHAU LÀ:
-6/3 VÀ 4/-8
3/-6 VÀ -8/4
-6/-8 VÀ 4/3
-8/-6 VÀ 3/4


ta có các phân số đố là
3/6 = 2/4
3/2=6/4
4/6 = 2/3
4/2 = 6/3