
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\widehat{B}+\widehat{C}=90^0\)
c: Góc kề bù với C bằng tổng của góc A cộng góc B

\(\dfrac{x}{-3}=\dfrac{y}{7}\Rightarrow\dfrac{x}{6}=\dfrac{y}{-14};\dfrac{y}{-2}=\dfrac{z}{5}\Rightarrow\dfrac{y}{-14}=\dfrac{z}{35}\\ \Rightarrow\dfrac{x}{6}=\dfrac{y}{-14}=\dfrac{z}{35}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{-14}=\dfrac{z}{35}=\dfrac{2x}{12}=\dfrac{4y}{-56}=\dfrac{5z}{175}=\dfrac{-2x-4y+5z}{-12+56+175}=\dfrac{146}{219}=\dfrac{2}{3}\\ \Rightarrow\left\{{}\begin{matrix}x=6\cdot\dfrac{2}{3}=4\\y=-14\cdot\dfrac{2}{3}=-\dfrac{28}{3}\\z=35\cdot\dfrac{2}{3}=\dfrac{70}{3}\end{matrix}\right.\)
x/-3=y/7;y/-2=z/5 và -2x-4y+5z=146
BCNN(7,2)=14
=>x/-3=y/7;y/-2=z/5
=>x/-3=y/7=>x/6=y/14(1)
=>y/-2=z/5=>y/-14=z/35(2)
từ(1) và (2) =>x/6=y/-14=z/35 và -2x-4y+5z=146
Sử dụng tính chất dãy tỉ số bằng nhau:
=>x/6=y/-14=z/35=>-2x-4y+5z/(-2).6-4.(-14)+5.35=146/219=2/3
=>x/6=2/3=>x=2.6/3=4
=>y/-14=2/3=>y=-14.2/3=-28/3
=>z/35=2/3=>z=35.2/3=70/3


Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)

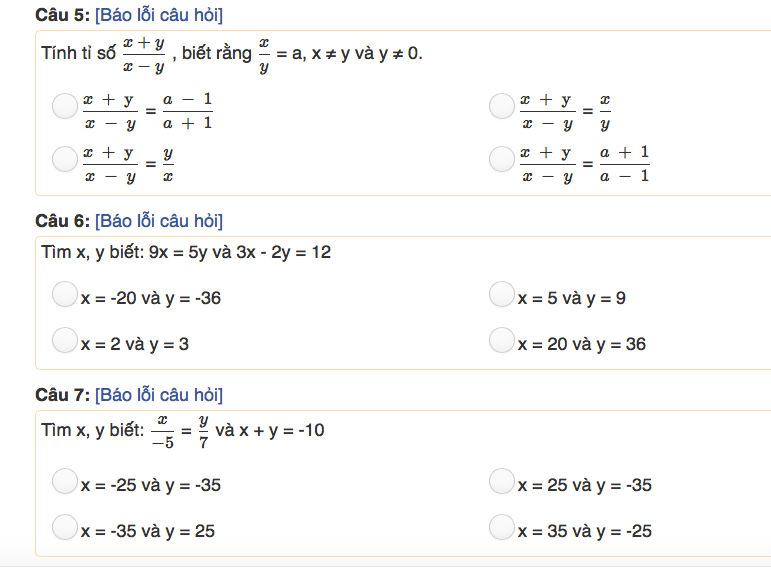
Câu 5:
\(\dfrac{x}{y}=a\Rightarrow\dfrac{x}{a}=\dfrac{y}{1}=\dfrac{x-y}{a-1}=\dfrac{x+y}{a+1}\)
\(\Rightarrow\dfrac{x+y}{x-y}=\dfrac{a+1}{a-1}\)
Câu 6:
\(9x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)
\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{3x}{15}=\dfrac{2y}{18}=\dfrac{3x-2y}{15-18}=\dfrac{12}{-3}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-4\right).5=-20\\y=\left(-4\right).9=-36\end{matrix}\right.\)
Câu 7:
\(\dfrac{x}{-5}=\dfrac{y}{7}=\dfrac{x+y}{-5+7}=\dfrac{-10}{2}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-5\right).\left(-5\right)=25\\y=\left(-5\right).7=-35\end{matrix}\right.\)

b: \(\sqrt{8^2+6^2}-\sqrt{16}+\dfrac{1}{2}\sqrt{\dfrac{4}{25}}\)
\(=10-4+\dfrac{1}{2}\cdot\dfrac{2}{5}=6+\dfrac{1}{5}=\dfrac{31}{5}\)

b) Vì \(\hept{\begin{cases}2a=3b\\4b=5c\end{cases}}\Rightarrow\hept{\begin{cases}\frac{a}{3}=\frac{b}{2}\\\frac{b}{5}=\frac{c}{4}\end{cases}}\) \(\Rightarrow\hept{\begin{cases}\frac{a}{15}=\frac{b}{10}\\\frac{b}{10}=\frac{c}{8}\end{cases}}\Rightarrow\frac{a}{15}=\frac{b}{10}=\frac{c}{8}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{15}=\frac{b}{10}=\frac{c}{8}=\frac{2a}{30}=\frac{2c}{16}=\frac{2a-b-2c}{30-10-16}=\frac{4}{4}=1\)
\(\Rightarrow\hept{\begin{cases}a=15\\b=10\\c=8\end{cases}}\)
Câu 5 :
Vì \(\hept{\begin{cases}a=2b\\b=3c\end{cases}}\Rightarrow\hept{\begin{cases}\frac{a}{2}=\frac{b}{1}\\\frac{b}{3}=\frac{c}{1}\end{cases}}\)\(\Rightarrow\hept{\begin{cases}\frac{a}{6}=\frac{b}{3}\\\frac{b}{3}=\frac{c}{1}\end{cases}}\Rightarrow\frac{a}{6}=\frac{b}{3}=\frac{c}{1}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{6}=\frac{b}{3}=\frac{c}{1}=\frac{2b}{6}=\frac{3c}{3}=\frac{a-2b+3c}{6-6+3}=\frac{6}{3}=2\)
\(\Rightarrow\hept{\begin{cases}a=2.6=12\\b=2.3=6\\c=2.1=2\end{cases}}\)

5:
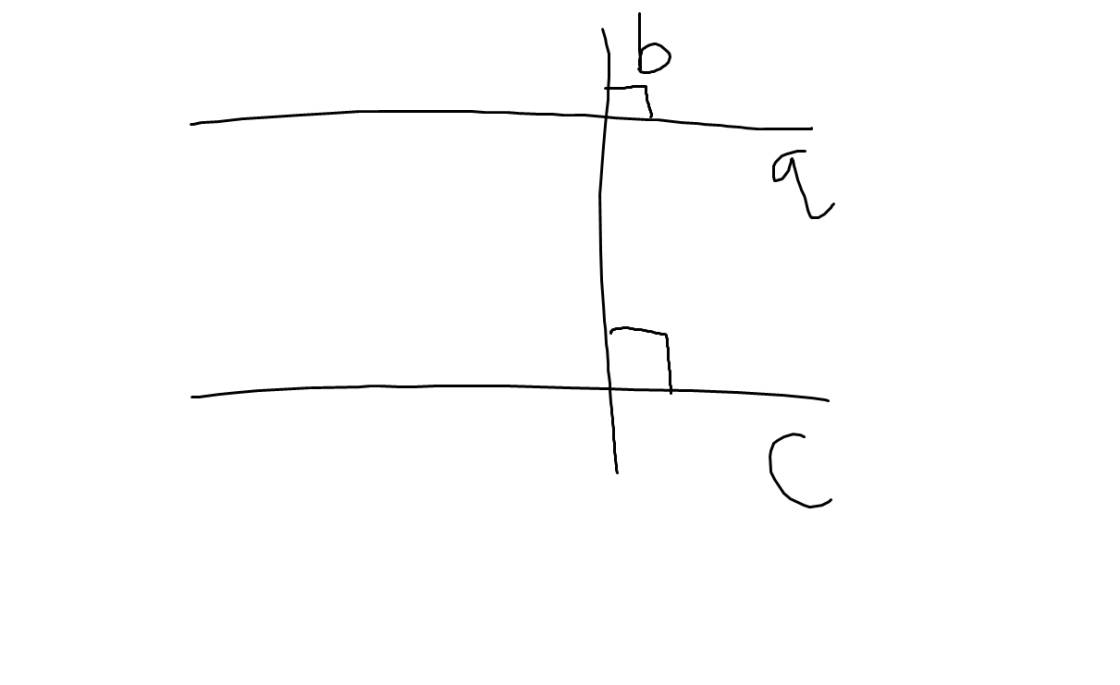
a: Giả thiết: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba
Kết luận: Hai đường thẳng đó song song
b:
| GT | a\(\perp\)b; b\(\perp\)c |
| KL | a//c |
6:
a: \(\widehat{A_1}\) đồng vị với \(\widehat{B_4}\)
góc A4 là góc so le trong với góc B4
b: \(\widehat{A_2}=\widehat{A_3}\)(hai góc đối đỉnh)
mà \(\widehat{A_3}=140^0\)
nên \(\widehat{A_2}=140^0\)
\(\widehat{A_2}=\widehat{B_3}\)(đồng vị, a//b)
mà \(\widehat{A_2}=140^0\)
nên \(\widehat{B_3}=140^0\)
c: \(\widehat{A_4}=180^0-140^0=40^0\)
ΔBHA vuông tại H
=>\(\widehat{HBA}+\widehat{HAB}=90^0\)
=>\(\widehat{HBA}=90^0-40^0=50^0\)

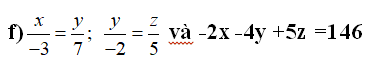 làm giúp mình với mình làm ơn đó ạ
làm giúp mình với mình làm ơn đó ạ

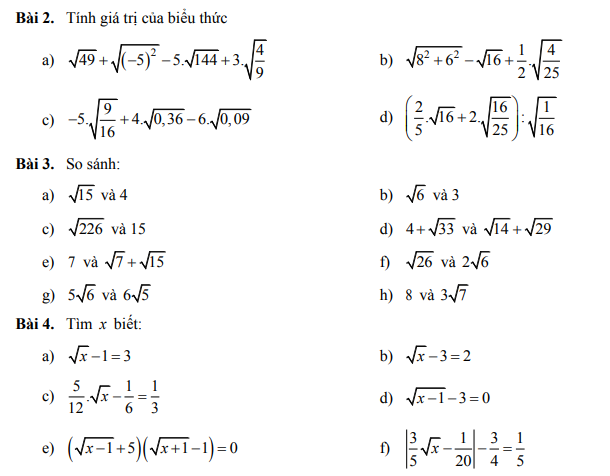 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy

bn thi đúng ko
Không ạ,đây là btvn á