
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x}{-3}=\dfrac{y}{7}\Rightarrow\dfrac{x}{6}=\dfrac{y}{-14};\dfrac{y}{-2}=\dfrac{z}{5}\Rightarrow\dfrac{y}{-14}=\dfrac{z}{35}\\ \Rightarrow\dfrac{x}{6}=\dfrac{y}{-14}=\dfrac{z}{35}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{-14}=\dfrac{z}{35}=\dfrac{2x}{12}=\dfrac{4y}{-56}=\dfrac{5z}{175}=\dfrac{-2x-4y+5z}{-12+56+175}=\dfrac{146}{219}=\dfrac{2}{3}\\ \Rightarrow\left\{{}\begin{matrix}x=6\cdot\dfrac{2}{3}=4\\y=-14\cdot\dfrac{2}{3}=-\dfrac{28}{3}\\z=35\cdot\dfrac{2}{3}=\dfrac{70}{3}\end{matrix}\right.\)
x/-3=y/7;y/-2=z/5 và -2x-4y+5z=146
BCNN(7,2)=14
=>x/-3=y/7;y/-2=z/5
=>x/-3=y/7=>x/6=y/14(1)
=>y/-2=z/5=>y/-14=z/35(2)
từ(1) và (2) =>x/6=y/-14=z/35 và -2x-4y+5z=146
Sử dụng tính chất dãy tỉ số bằng nhau:
=>x/6=y/-14=z/35=>-2x-4y+5z/(-2).6-4.(-14)+5.35=146/219=2/3
=>x/6=2/3=>x=2.6/3=4
=>y/-14=2/3=>y=-14.2/3=-28/3
=>z/35=2/3=>z=35.2/3=70/3

a: Xét ΔABE vuông tai A và ΔHBE vuông tại H có
BE chung
gócABE=gócHBE
=>ΔABE=ΔHBE
b: ΔBAE=ΔBHE
=>BA=BH; EA=EH
=>BE là trung trực của AH

a: \(\widehat{B}+\widehat{C}=90^0\)
c: Góc kề bù với C bằng tổng của góc A cộng góc B

b: \(=8+2\cdot3-7\cdot1.3+3\cdot\dfrac{5}{4}=8.65\)

a, \(\angle\left(A1\right)+\angle\left(A2\right)=180^o\left(ke-bu\right)=>\angle\left(A2\right)=180^0-60^0=120^o\)
\(=>\angle\left(A2\right)=\angle\left(B1\right)=120^o\)
mà 2 góc này ở vị trí so le trong \(=>Ax//By\)
b, \(\angle\left(B3\right)+\angle\left(C\right)=130^o+50^0=180^o\)
mà 2 góc ở vị trí trong cùng phía \(=>By//Cz\)


\(x-y\) = 0,4
\(x\) = 0,4 + y
⇒ \(\dfrac{5.\left(0,4+y\right)+7}{2}\) = \(\dfrac{2y-9}{5}\)
⇒5.[5.(0,4 +y) + 7] = (2y - 9).2
⇒ 10 + 25y + 35 = 4y - 18
25y - 4y = - 10 - 35 - 18
21y = - 63
y = -3
\(x\) = -3 + 0,4 = -2,6
\(\dfrac{4y+3}{3}\) = \(\dfrac{3z-y}{5}\)
\(\dfrac{4.\left(-3\right)+3}{3}\) = \(\dfrac{3z-3}{5}\)
-3 = 3.( \(\dfrac{z-1}{5}\))
z - 1 = 3 : \(\dfrac{3}{5}\)
z - 1 = 5
z = 6
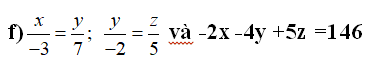 làm giúp mình với mình làm ơn đó ạ
làm giúp mình với mình làm ơn đó ạ



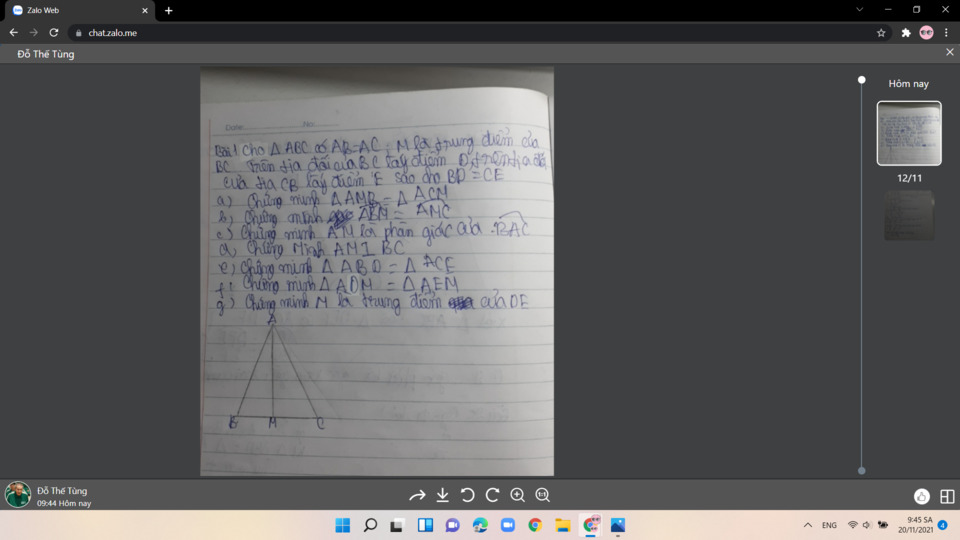
 làm giúp mình bài 1 với, mình cần gấp ( nếu rảnh làm hộ mình bài 2 cũng dc )
làm giúp mình bài 1 với, mình cần gấp ( nếu rảnh làm hộ mình bài 2 cũng dc )
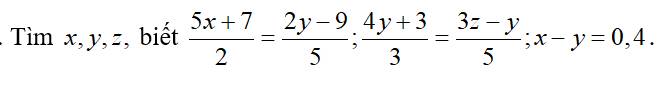
Bài 4 :
a, Áp dụng Py ta go cho tam giác AHB
\(AH^2+HB^2=AB^2\Leftrightarrow12^2+9^2=AB^2\)
\(\Leftrightarrow144+81=AB^2\Leftrightarrow AB^2=225\Leftrightarrow AB=15\)cm
Áp dụng Py ta go cho tam giác AHC ( đề phải là tính AC nhé ! )
\(AH^2+HC^2=AC^2\Leftrightarrow12^2+20^2=AC^2\)
\(\Leftrightarrow144+400=AC^2=\Leftrightarrow AC^2=544\Leftrightarrow AC=4\sqrt{34}\)