

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


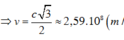

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

v = 0,8c
Chiều dài thước trong hệ quy chiếu đứng yên đo được là
\(l=l_0\sqrt{1-\left(\frac{v}{c}\right)^2}=0,6m\)
độ co là 40cm
-----> chọn B

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

\(W_{đ} = mc^2-m_0c^2= m_0c^2 (\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}-1)\)
mà \(W_{đ} = m_0c^2\)
=> \( \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}-1=1\)
=> \( 1-\frac{v^2}{c^2}=0,25\)
=> \(v^2 = 0 ,75 c^2 \)
=> \(v = 2,6.10^{8} (m/s).\)

\(m = \frac{m_ 0}{\sqrt{1-\frac{v^2}{c^2}}} = \frac{m_0}{\sqrt{1-0,6^2}} = 1,25 m_0.\)