Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

E, F là trung điểm của AD và BC (đề bài) => EF là đường trung bình của ht ABCD => EF//AB//CD
+ Xét tg ABD có
E là trung điểm AD (đề bài)
EI//AB
=> EI là đường trung bình của tg ABD => EI=AB/2 (1)
+ Xét tg ABC chứng minh tương tự cũng có KF=AB/2 (2)
Từ (1) và (2) => EI=KF
+ Xét tg BCD chứng minh tương tự có IF=(IK+KF)=CD/2
\(\Rightarrow IF-EI=IK+KF-EI=IK=\frac{CD}{2}-\frac{AB}{2}=\frac{CD-AB}{2}.\)
b/ Câu b dựa vào KQ của câu a

a: Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng với ΔOCD
=>OA/OC=OB/OD=AB/CD
=>OA/10=OC/18=(OA+OC)/(10+18)=21/28=3/4
=>OA=7,5cm; OC=13,5cm
b: OA/OC=OB/OD
=>OA*OD=OB*OC
c: AM/CN=AB/CD=OA/OC
Xét ΔOAM và ΔOCN có
OA/OC=AM/CN
góc OAM=góc OCN
=>ΔOAM đồng dạng với ΔOCN
=>góc AOM=góc CON
=>góc AOM+góc AON=180 độ
=>M,O,N thẳng hàng


Hạ \(BK\perp DH\left(K\in DH\right);\text{AF}\perp DH\left(F\in DH\right)\)
\(\Delta ADF=\Delta BCK\left(c.h-g.n\right)\)nên \(DF=CK\)
\(AB//FK;\text{AF}//BK\rightarrow AB=FK\)
Do đó :
\(KC=\frac{CD-AB}{2}=3\rightarrow DK=7\)
\(BH//EH;BD=BE\rightarrow DK=KH=\dfrac{DH}{2}=14\rightarrow SH=4\)

a.\(EF=\dfrac{AB+CD}{2}=\dfrac{6+10}{2}=8\left(cm\right)\)
b. Xét \(\Delta ADC:\)
có: EK//DC =>\(\dfrac{AE}{ED}=\dfrac{AK}{KC}=1\Rightarrow AK=KC\)
Xét \(\Delta BDC\):
có: IF//DC => \(\dfrac{BF}{FC}=\dfrac{BI}{ID}=1\Rightarrow BI=ID\)
c.Xét \(\Delta DAB\)
có EI//AB=> \(\dfrac{ED}{AB}=\dfrac{EI}{AB}=\dfrac{1}{2}\Rightarrow EI=\dfrac{AB}{2}=3\left(cm\right)\)
Xét \(\Delta ABC\)
có KF//AB=> \(\dfrac{FC}{BC}=\dfrac{KF}{AB}=\dfrac{1}{2}\Rightarrow FK=\dfrac{AB}{2}=3\left(cm\right)\)
\(\Rightarrow IK=\text{EF}-3.2=2\left(cm\right)\)
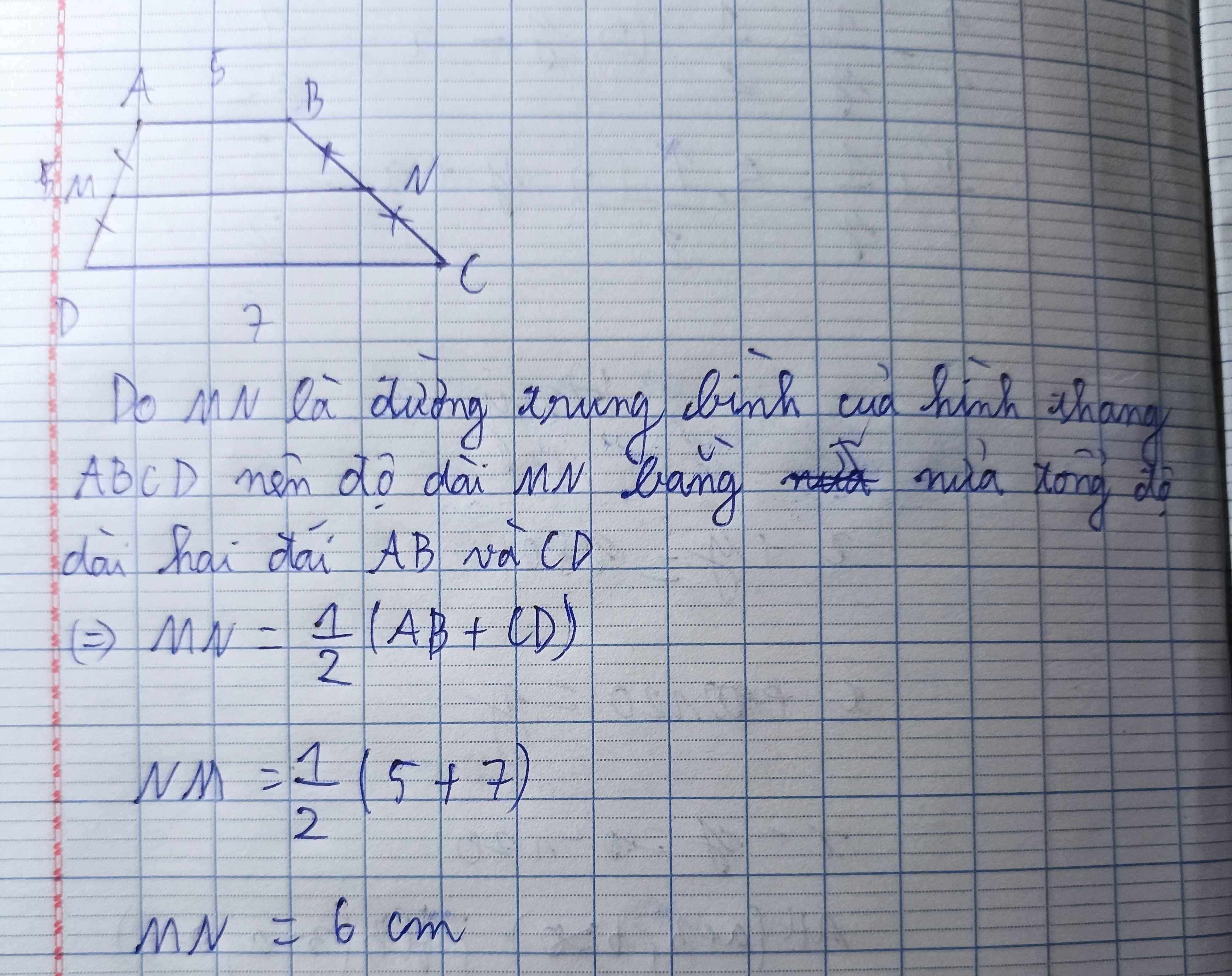
Hình vẽ:
Giải:
Theo tính chất đường trung bình trong hình thang, ta có:
\(MN=\dfrac{AB+CD}{2}\)
\(\Leftrightarrow MN=\dfrac{4+7}{2}=\dfrac{11}{2}=5,5\left(cm\right)\)
Vậy dộ dài cạnh MN là 5,5 cm.
Theo tính chất đường trung bình trong hình thang, ta có:
\(MN=\dfrac{AB+CD}{2}\)
\(\Leftrightarrow MN=\dfrac{4+7}{2}=\dfrac{11}{2}=5,5\left(cm\right)\)
Vậy dộ dài cạnh MN là 5,5 cm.