
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Bạn đọc lại sách vừa đọc vừa xem ví dụ là được. Chứ không gặp trực tiếp thì giảng bằng cách nào

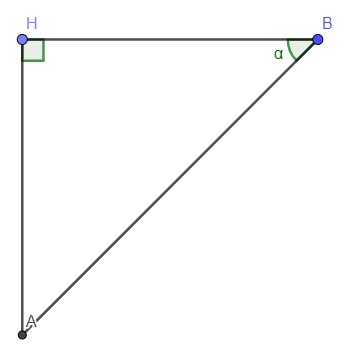
chứng minh: \(1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
xét VT: \(1+tg^2\alpha=1+\dfrac{sin^2\alpha}{cos^2\alpha}\left(vì:tg\left(\alpha\right)=\dfrac{sin\left(\alpha\right)}{cos\left(\alpha\right)}\right)\)
\(=\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}=\dfrac{1}{cos^2\alpha}\left(vì:sin^2\alpha+cos^2\alpha=1\right)=VP\Rightarrow1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
\(\Leftrightarrow1+\dfrac{AH^2}{50^2}=\dfrac{1}{\left(\dfrac{AH^2}{AB^2}\right)}=\dfrac{AB^2}{AH^2}\Leftrightarrow\dfrac{2500+AH^2}{2500}=\dfrac{AB^2}{AH^2}\Leftrightarrow2500AH^2+AH^4=2500AB^2\left(1\right)\)
ta có: \(AH^2+BH^2=AB^2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow2500AH^2+AH^4=2500\left(AH^2+50^2\right)\Leftrightarrow AH^4=2500.2500=50^4\Leftrightarrow AH=50\left(m\right)\left(3\right)\)
\(\left(2\right)\left(3\right)\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{50^2+50^2}=50\sqrt{2}\left(m\right)\)
vậy chiều rộng con sông là: \(AH=50\left(m\right)\) và quãng đường đò đã đi là \(AB=50\sqrt{2}\left(m\right)\)

Lúc đầu kho a hơn kho b số tấn thóc là:
15 + 15 + 12 = 42 (tấn)
Số thóc kho a lúc đầu là:
(750 + 42) : 2 = 396 (tấn)
Số thóc kho b lúc đầu là:
750 - 396 = 354 (tấn)
Đáp số: Kho a: 396 tấn
Kho b: 354 tấn
nếu chuyển từ kho a sang kho b 15 tấn thì tổng số thóc ở hai kho không thay đổi
số thóc ở kho a sau khi chuyển từ kho a sang kho b 15 tấn là
[750+12]:2=381 tấn
số thóc ở kho a lúc đầu là
381+15=396 tấn
số thóc ở kho b lúc đầu là
750-396=354 tấn
trả lời :
bài bé quá bn òi
mk ko nhìn thấy
Bài bé quá, bn đăng lại câu hỏi đi