Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/
Xét tg vuông AHD và tg vuông EHD có
HA=HD (gt); DH chung => tg AHD = tg EHD (hai tg vuông có 2 cạnh góc vuông bằng nhau)
\(\Rightarrow\widehat{DAH}=\widehat{DEH}\)
Xét tg vuông AHD có
\(\widehat{DAH}=90^o-\widehat{ADH}=90^o-30^o=60^o\)
\(\Rightarrow\widehat{DAH}=\widehat{DEH}=60^o\)
Xét tg ADE có
\(\widehat{ADE}=180^o-\left(\widehat{DAH}+\widehat{DEH}\right)=180^o-\left(60^o+60^o\right)=60^o\)
\(\Rightarrow\widehat{DAH}=\widehat{DEH}=\widehat{ADE}=60^o\)
=> tg ADE là tg đều
2/
Xét tg vuông AHD có
\(AH=\dfrac{AD}{2}=\dfrac{8}{2}=4cm\) (trong tg vuông cạnh đối diện góc \(30^o\) bằng nửa cạnh huyền)
\(\Rightarrow AH=EH=4cm\Rightarrow AH+EH=AE=8cm\)
\(DH=\sqrt{AD^2-AH^2}=\sqrt{8^2-4^2}=4\sqrt{3}cm\) (Pitago)
\(\Rightarrow S_{ADE}=\dfrac{1}{2}.AE.DH=\dfrac{1}{2}.8.4\sqrt{3}=16\sqrt{3}cm^2\)
\(\Rightarrow S_{ABCD}=\dfrac{\left(AB+CD\right).AH}{2}=\dfrac{\left(7+10\right).4}{2}=34cm^2\)

. a) HS tự chứng minh
b) Kẻ đường cao AH, BK,chứng minh được DH = CK
Ta được H D = C D − A B 2 = 3 c m
Þ AH = 4cm Þ SABCD = 20cm2

Bài 5
\(\widehat{A}+\widehat{D}=180^o\) (Hai góc trong cùng phía bù nhau)
\(\widehat{DAx}=\widehat{BAx}=\dfrac{\widehat{A}}{2}\) (gt)
\(\widehat{ADy}+\widehat{CDy}=\dfrac{\widehat{D}}{2}\) (gt)
\(\Rightarrow\widehat{DAx}+\widehat{ADy}=\dfrac{\widehat{A}}{2}+\dfrac{\widehat{D}}{2}=\dfrac{180^o}{2}=90^o\)
Xét tg ADE có
\(\widehat{AED}=180^o-\left(\widehat{DAx}+\widehat{ADy}\right)=180^o-90^o=90^o\) (Tổng các góc trong của tg bằng 180 độ)
\(\Rightarrow Ax\perp Dy\)
Bài 6:
a/
Ta có
AB//CD => AB//DE
BE//AB (gt)
=> ABED là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> AB = DE; AD = BE (Trong hình bình hành các cạnh đối nhau thì bằng nhau)
b/
CD - DE = CE
Mà AB = DE (cmt)
=> CD - AB = CE
c/
Xét tg BCE có
BC+BE>CE (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)
Mà CE = CD - DE và DE = AB (cmt) và BE = AD
=> BC+BE = BC + AD>CE = CD - AB
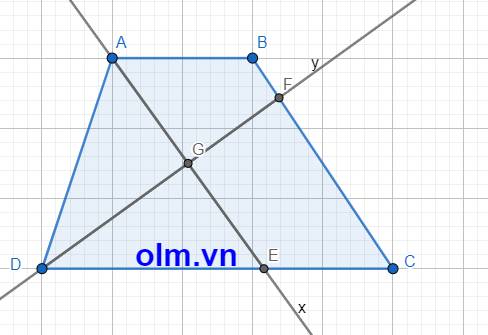
Gọi G là giao điểm của hai đường phân giác Ax và By
Ta có: \(\widehat{ADG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) ( vì DG là phân giác góc ADE)
\(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{DAB}\)( vì AG là phân giác góc DAB )
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) + \(\dfrac{1}{2}\)\(\widehat{DAB}\) = \(\dfrac{1}{2}\)(\(\widehat{ADE}\) + \(\widehat{DAB}\))
\(\widehat{ADE}\) + \(\widehat{DAB}\) = 1800 (vì hai góc là hai góc trong cùng phía)
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\) \(\times\) 1800 = 900
Xét tam giác ADG có: \(\widehat{GAD}\) + \(\widehat{ADG}\) + \(\widehat{DGA}\) = 1800 (tổng ba góc trong 1 tam giác bằng 1800)
⇒ \(\widehat{DGA}\) = 1800 - 900 = 900
Vậy tam giác ADG vuông tại G ⇒AE \(\perp\) DG (đpcm)
CôLoan ơi em sắp thi HSG rồi, đề ôn câu 5 đ đó, cô ko giúp là em chết mất