
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\widehat{B}=45^0\)
\(b=c=10cm\)
\(a=\sqrt{2\cdot b^2}=10\sqrt{2}\left(cm\right)\)
b: \(\widehat{C}=90^0-35^0=55^0\)
\(b=a\cdot\sin B=11,47\left(cm\right)\)
\(c=\sqrt{a^2-b^2}=16,38\left(cm\right)\)

\(a+b+c=0\Rightarrow c=-\left(a+b\right);\left(1\right)\)
\(ab+bc+ca=0\Rightarrow ab+c\left(a+b\right)=0;\left(2\right)\)
(1)(2)=>\(ab=c^2\)
tương tự trên
=>\(bc=a^2\)và \(ca=b^2\)
\(ab+bc+ca=0\Leftrightarrow c^2+a^2+b^2=0\Rightarrow a=b=c=0\)
=> M = 2



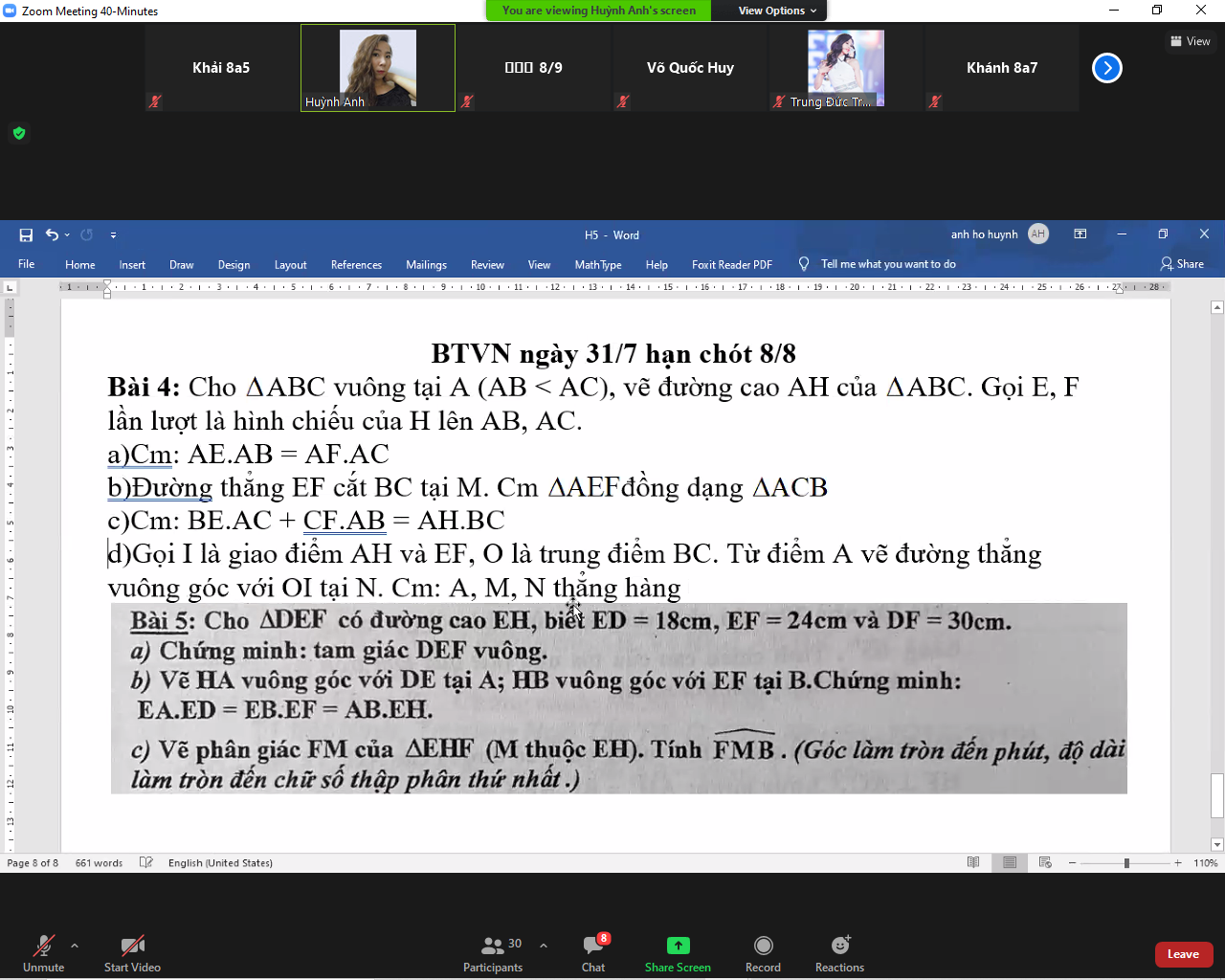
Bài 5:
a) Xét ΔDEF có \(DF^2=ED^2+EF^2\left(30^2=18^2+24^2\right)\)
nên ΔDEF vuông tại E(Định lí Pytago đảo)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔEHD vuông tại H có HA là đường cao ứng với cạnh huyền ED, ta được:
\(EA\cdot ED=EH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔEHF vuông tại H có HB là đường cao ứng với cạnh huyền EF, ta được:
\(EB\cdot EF=EH^2\)(2)
Xét tứ giác EAHB có
\(\widehat{BEA}=90^0\)
\(\widehat{EBH}=90^0\)
\(\widehat{EAH}=90^0\)
Do đó: EAHB là hình chữ nhật
Suy ra: EH=BA
hay \(EH\cdot BA=EH^2\)(3)
Từ (1), (2) và (3) suy ra \(EA\cdot ED=EB\cdot EF=EH\cdot BA\)



Câu 2:
a) Ta có: \(\sqrt{9x^2-12x+4}-7=0\)
\(\Leftrightarrow\left|3x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-2=7\\3x-2=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=9\\3x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{3}\end{matrix}\right.\)
b) Ta có: \(3\sqrt{4x-12}=15+\dfrac{1}{3}\sqrt{9x-27}\)
\(\Leftrightarrow6\sqrt{x-3}-\sqrt{x-3}=15\)
\(\Leftrightarrow5\sqrt{x-3}=15\)
\(\Leftrightarrow\sqrt{x-3}=3\)
\(\Leftrightarrow x-3=9\)
hay x=12



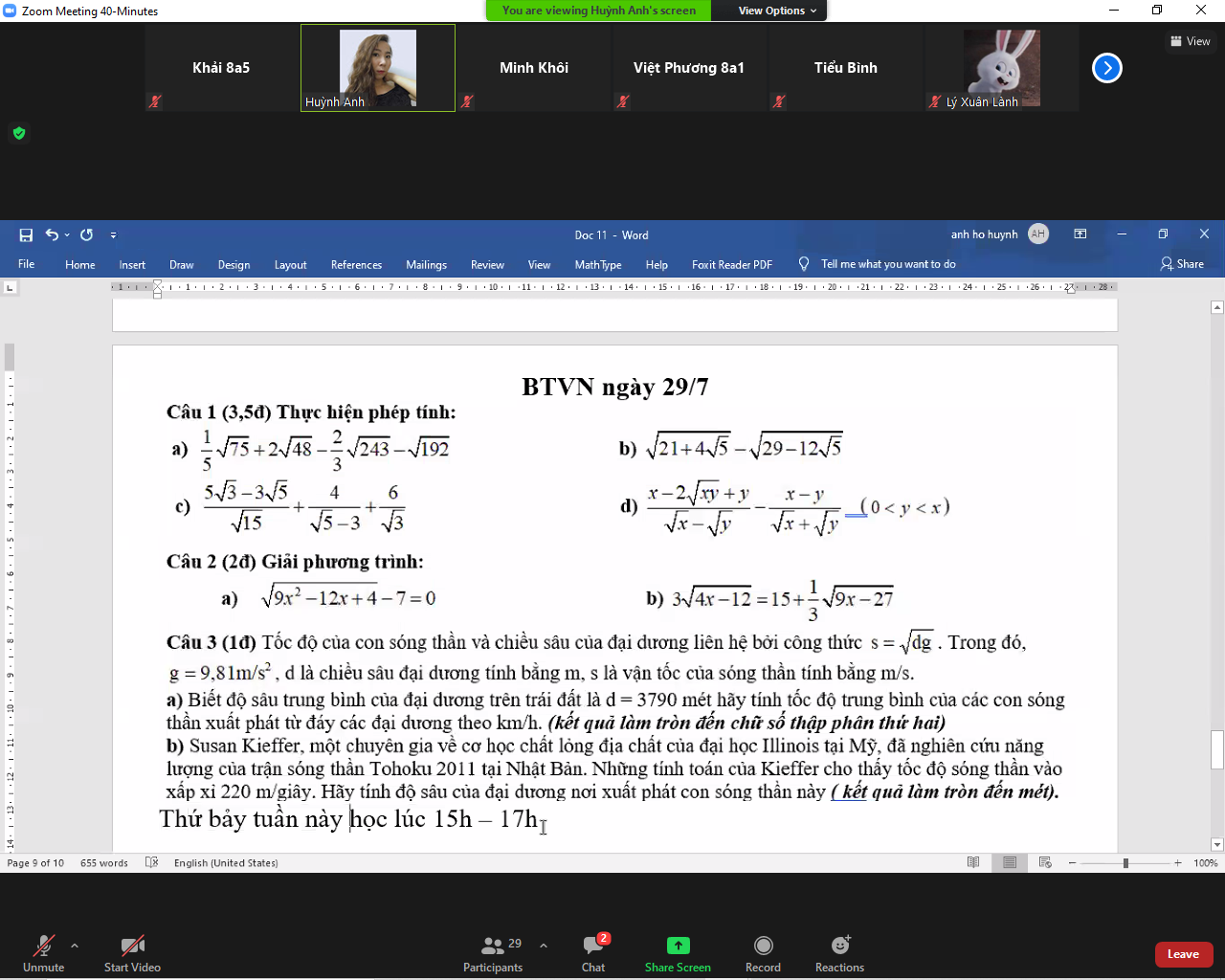 help em cau 3 vs
help em cau 3 vs