K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 10 2021
\(a,ĐK:x\le2\\ PT\Leftrightarrow x^2-x-8=4-2x\Leftrightarrow x^2+x-12=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=-4\left(tm\right)\end{matrix}\right.\Leftrightarrow x=-4\\ b,ĐK:5x^2+10x+1\ge0\\ PT\Leftrightarrow5x^2+10x+1=\left(7-x^2-2x\right)^2\\ \Leftrightarrow5x^2+10x+1=x^4+4x^2+49-14x^2+4x^3-28x\\ \Leftrightarrow x^4+4x^3-15x^2-38x+48=0\\ \Leftrightarrow x^4-x^3+5x^3-5x^2-10x^2+10x-48x+48=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+5x^2-10x-48\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+3x^2+2x^2+6x-16x-48\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+3\right)\left(x^2+2x-16\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\\x^2+2x-16=0\left(1\right)\end{matrix}\right.\)
\(\Delta\left(1\right)=4+64=68\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-2-2\sqrt{17}}{2}=-1-\sqrt{17}\\x=\dfrac{-2+2\sqrt{17}}{2}=-1+\sqrt{17}\end{matrix}\right.\)
Vậy pt có nghiệm ...
AH
Akai Haruma
Giáo viên
31 tháng 7 2021
Bài 1:
Nếu chị nhớ không nhầm thì phải là \(\left[\begin{matrix} \frac{1}{2}\leq x< 2\\ 0< x<\frac{1}{2}\end{matrix}\right.\)
Tức là $x$ nhận các khoảng giá trị sau:
\(0< x< \frac{1}{2}\); \(x=\frac{1}{2}\); \(\frac{1}{2}< x< 2\)
Vậy có nghĩa $0< x< 2$ (rất dễ hiểu mà????)
AH
Akai Haruma
Giáo viên
31 tháng 7 2021
Bài 2:
Ngoặc nhọn dùng khi muốn biểu thị hai/ nhiều phương trình/ bất phương trình đồng thời xảy ra cùng một lúc
Ngoặc vuông dùng khi muốn biểu thị cái này hoặc cái kia xảy ra.
Bài trên phải dùng ngoặc vuông là sao em? Ngoặc nhọn thường xuất hiện trong bài toán giải hệ phương trình, bất phương trình. Còn ngoặc vuông thì thường dùng kết luận nghiệm của pt/ bpt.
Kết hợp điều kiện thì dùng ngoặc nhọn. Ví dụ $\sqrt{x+1}+\sqrt{2-x}$ thì việc $x+1\geq 0$ và $2-x\geq 0$ phải đồng thời xảy ra cùng lúc.
HV
3
KL
5
21 tháng 1 2018
nhiều lắm nhớ sao được có hơn 20 cái hằng đẳng thức mà tự tra google đi
16 tháng 12 2023
Câu 4:
1: Gọi AB là chiều cao của tháp; D,C lần lượt là điểm mà anh trên tháp thấy xe máy đang chạy.
Theo đề, ta có: AB=100m; AB\(\perp\)DB tại B; \(\widehat{ADB}=30^0;\widehat{ACB}=60^0\)
Xét ΔABD vuông tại B có \(sinD=\dfrac{AB}{AD}\)
=>\(\dfrac{100}{AD}=sin30=\dfrac{1}{2}\)
=>\(AD=200\left(m\right)\)
Ta có: ΔABD vuông tại B
=>\(BA^2+BD^2=AD^2\)
=>\(BD^2=200^2-100^2=30000\)
=>\(BD=100\sqrt{3}\left(m\right)\)
Ta có: \(\widehat{ACB}+\widehat{ACD}=180^0\)(hai góc kề bù)
=>\(\widehat{ACD}=180^0-60^0=120^0\)
Xét ΔCAD có \(\widehat{D}+\widehat{ACD}+\widehat{CAD}=180^0\)
=>\(\widehat{CAD}+120^0+30^0=180^0\)
=>\(\widehat{CAD}=30^0\)
Xét ΔCAD có \(\dfrac{AD}{sinACD}=\dfrac{DC}{sinDAC}\)
=>\(\dfrac{200}{sin120}=\dfrac{DC}{sin30}\)
=>\(DC=\dfrac{200\sqrt{3}}{3}\left(m\right)\)
=>Sau 6 phút thì xe máy đi được quãng đường là \(\dfrac{200\sqrt{3}}{3}\left(m\right)\)
Vận tốc của xe máy là: \(\dfrac{200\sqrt{3}}{3}:6=\dfrac{200\sqrt{3}}{18}=\dfrac{100\sqrt{3}}{9}\left(\dfrac{m}{p}\right)\)
Thời gian xe máy đến chân tháp là:
\(100\sqrt{3}:\dfrac{100\sqrt{3}}{9}=9\left(phút\right)\)
2:
a: ΔDAC vuông tại D
=>\(AC^2=DA^2+DC^2\)
=>\(AC^2=6^2+8^2=100\)
=>\(AC=\sqrt{100}=10\left(cm\right)\)
Xét ΔDAC vuông tại D có DH là đường cao
nên \(DH\cdot AC=DA\cdot DC\)
=>\(DH\cdot10=6\cdot8=48\)
=>DH=48/10=4,8(cm)
Xét ΔADC vuông tại D có \(sinACD=\dfrac{AD}{AC}=\dfrac{6}{10}=\dfrac{3}{5}\)
nên \(\widehat{ACD}\simeq36^052'\)
b: Xét ΔDAC vuông tại D có DH là đường cao
nên \(AH\cdot AC=AD^2;CH\cdot CA=CD^2\)
=>\(\dfrac{AH\cdot AC}{CH\cdot AC}=\dfrac{AD^2}{CD^2}\)
=>\(\dfrac{AH}{CH}=\dfrac{BC^2}{AB^2}=\left(\dfrac{BC}{AB}\right)^2\)
c: Gọi K là trung điểm của DH
Xét ΔHAD có
F,K lần lượt là trung điểm của HA,HD
=>FK là đường trung bình của ΔHAD
=>FK//AD và \(FK=\dfrac{AD}{2}\)
ta có: FK//AD
AD\(\perp\)DC
Do đó: FK\(\perp\)DC
Xét ΔFDC có
FK,DH là các đường cao
FK cắt DH tại K
Do đó: K là trực tâm của ΔFDC
=>FK\(\perp\)DC
Ta có: FK//AD
BC//AD
Do đó: FK//BC
Ta có: \(FK=\dfrac{AD}{2}\)
\(CE=\dfrac{CB}{2}\)
mà AD=CB
nên FK=CE
Xét tứ giác FKCE có
FK//CE
FK=CE
Do đó: FKCE là hình bình hành
=>CK//FE
Ta có: CK//FE
CK\(\perp\)FD
Do đó: FE\(\perp\)FD
3 tháng 7 2021
B1)
b, Có \(x\ge0\Rightarrow B=x+\sqrt{x}+4\ge0+0+4=4\)
Dấu "=" xảy ra khi x=0
Vậy \(B_{min}=4\)
3 tháng 7 2021
Bài 1 :
\(b,B=x+\sqrt{x}+4=x+2.\sqrt{x}.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{15}{4}\)
\(=\left(\sqrt{x}+\dfrac{1}{2}\right)^2+\dfrac{15}{4}\)
Thấy : \(\sqrt{x}+\dfrac{1}{2}\ge\dfrac{1}{2}\)
\(\Rightarrow B=\left(\sqrt{x}+\dfrac{1}{2}\right)^2+\dfrac{15}{4}\ge4\)
Vậy \(Min_B=4\Leftrightarrow x=0\)
MT
Căn x >-1 thì có tìm được x không ạ. Nếu được giải ra giúp mình nhá còn không thì chỉ là tại sao nhá
1
19 tháng 7 2021
\(\sqrt{x}>-1=>\sqrt{x}+1>0\)(1)
ta thấy \(\sqrt{x}\ge0=>\sqrt{x}+1\ge1\left(2\right)\)
(1)(2)=>vô lí nên ko tìm đc x
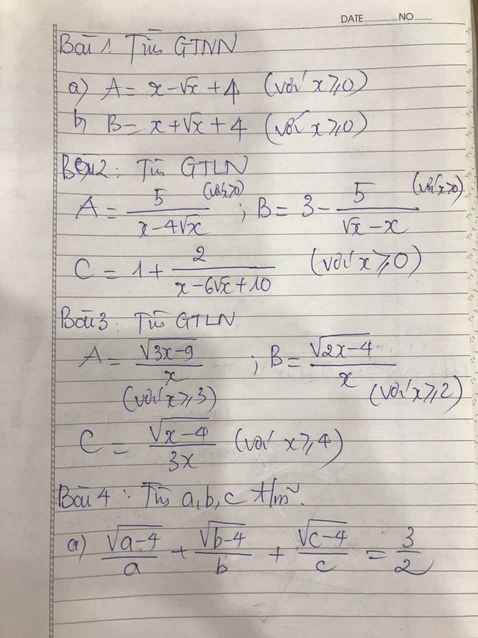
ddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddđ3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333332222222222222222222222222222222222222222222222222222222222mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppp55555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555uuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111119999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999