
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


dấu bằng xảy ra khi :
\(x+\dfrac{16}{x-2}=10\\ \Rightarrow x\left(x-2\right)+16=10x-20\\ x^2-2x+16=10x-20\\ x^2-12x+36=0\\ \left(x-6\right)^2=0\\ \Rightarrow x=6\)

a: Thay x=1 và y=-2 vào y=ax+1, ta được:
a+1=-2
hay a=-3
Vậy: (d'): y=-3x+1
c: Tọa độ giao điểm của (d) và (d') là:
\(\left\{{}\begin{matrix}-3x+1=x+3\\y=x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=3-\dfrac{1}{2}=\dfrac{5}{2}\end{matrix}\right.\)


\(a,\left(d\right)\)//\(\left(d'\right)\)\(\Leftrightarrow\left\{{}\begin{matrix}2m-3=m\\-m+2\ne3m-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow m=3\)
b, (d) cắt (d') \(\Leftrightarrow2m-3\ne m\Leftrightarrow m\ne3\)

Gọi x (chiếc) là số tàu dự định của đội (x∈N,0<x<140)
Số tàu tham gia vận chuyển là x+1 chiếc
Số tấn hàng trên mỗi chiếc dự định là280/x tấn
Số tấn hàng trên mỗi chiếc thực tế là 286/x+1 tấn
Theo bài ra ta có phương trình : 280/x−286/x+1=2
Giải phương trình được x=10 hoặc x=−14(Loại do x>0)
Vậy có 10 chiếc tàu

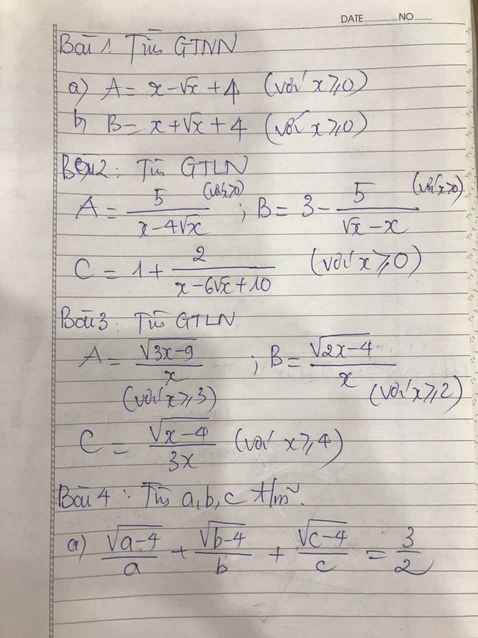
 mình dở toán hình lắm
mình dở toán hình lắm
B1)
b, Có \(x\ge0\Rightarrow B=x+\sqrt{x}+4\ge0+0+4=4\)
Dấu "=" xảy ra khi x=0
Vậy \(B_{min}=4\)
Bài 1 :
\(b,B=x+\sqrt{x}+4=x+2.\sqrt{x}.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{15}{4}\)
\(=\left(\sqrt{x}+\dfrac{1}{2}\right)^2+\dfrac{15}{4}\)
Thấy : \(\sqrt{x}+\dfrac{1}{2}\ge\dfrac{1}{2}\)
\(\Rightarrow B=\left(\sqrt{x}+\dfrac{1}{2}\right)^2+\dfrac{15}{4}\ge4\)
Vậy \(Min_B=4\Leftrightarrow x=0\)