Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tỉ số \(\frac{U}{I}\) ở mỗi vật dẫn là khác nhau vì điện trở của mỗi loại vật dẫn khác nhau
R = \(\frac{U}{I}\)
Ta có: \(R=\dfrac{U}{I}\) nên có thể vẽ giả sử: \(U_1=U_2\)
\(\Rightarrow R_1>R_2\)
\(\Rightarrow I_1< I_2\)
Suy ra độ dốc của đường đặc trưng ứng với R1 nhỏ hơn so với độ dốc của đường đặc trưng ứng với R2
a) F=k.|q1q2| / r2
<=> F = 9.109.|2.1,6.10-19.1,6.10-19| / ( 2,94.10-11)2
<=>F = 5,33.10-7
( mình giúp được câu a thôi nhé )
• Vật (chất) dẫn điện là chất mà điện tích có thể tự do di chuyển khắp mọi điểm của vật làm bằng chất đó.
• Vật (chất) Chất cách điện (hay điện môi) là những chất mà điện tích không di chuyển được từ nơi này sang nơi khác bên trong vật làm bằng chất đó.
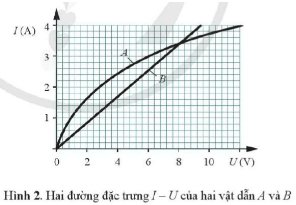
a) Đường đặc trưng của B là đường thẳng đi qua gốc tọa độ, biểu thị hàm số bậc nhất hay \(R=\dfrac{U}{I}=const\),
điện trở là hằng số. Do đó, vật dẫn B là đoạn dây thép.
b) Từ đồ thị, ta thấy, hai đường đặc trưng cắt nhau tại điểm (8;3,4). Tại đó \(U=8V\) và \(I=3,4A\)
Điện trở của mỗi vật dẫn ở hiệu điện thế này là: \(R=\dfrac{U}{I}=\dfrac{8}{3,4}\approx2,35\Omega\)
Q R q
Để chứng minh công thức trên thì ta tính theo định nghĩa: \(V=\dfrac{W_t}{q}\) (điện thế tại 1 điểm bằng thế năng tĩnh điện gây ra tại điện tích đặt ở điểm đó chia cho độ lớn điện tích).
Xét quả cầu có điện tích q đặt cách quả cầu Q một khoảng R.
Thế năng tĩnh điện do Q gây ra tại q là: \(W_t=\dfrac{kQq}{\varepsilon R}\)
Điện thế do Q gây ra tại vị trí q là: \(V=\dfrac{W_t}{q}=\dfrac{kQ}{\varepsilon R}\)
1. Tỉ số \(\dfrac{U}{I}\) đối với từng vật dẫn X và vật dẫn Y là không đổi.