Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1. Tỉ số \(\dfrac{U}{I}\) đối với từng vật dẫn X và vật dẫn Y là không đổi.
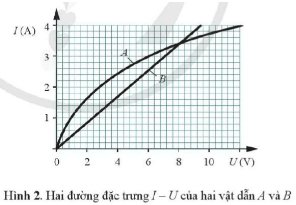
a) Đường đặc trưng của B là đường thẳng đi qua gốc tọa độ, biểu thị hàm số bậc nhất hay \(R=\dfrac{U}{I}=const\),
điện trở là hằng số. Do đó, vật dẫn B là đoạn dây thép.
b) Từ đồ thị, ta thấy, hai đường đặc trưng cắt nhau tại điểm (8;3,4). Tại đó \(U=8V\) và \(I=3,4A\)
Điện trở của mỗi vật dẫn ở hiệu điện thế này là: \(R=\dfrac{U}{I}=\dfrac{8}{3,4}\approx2,35\Omega\)
Ta có: \(R=\dfrac{U}{I}\) nên có thể vẽ giả sử: \(U_1=U_2\)
\(\Rightarrow R_1>R_2\)
\(\Rightarrow I_1< I_2\)
Suy ra độ dốc của đường đặc trưng ứng với R1 nhỏ hơn so với độ dốc của đường đặc trưng ứng với R2
Giả sử hai dây dẫn được đặt vuông góc với mặt phẳng hình vẽ, dòng I1 đi vào tại A,dòng I2 đi ra tại B.Các dòng điện I1và I2 gây ra tại M các véctơ cảm ứng từ tại \(\overrightarrow{B1}\) và \(\overrightarrow{B2}\) có phương chiều như hình vẽ, có độ lớn:
\(B1=B2=2.10^{-7}\frac{I1}{AM}=6.10^{-6}T\)
+Cảm ứng từ tổng hợp tại M là: \(\overrightarrow{B}=\overrightarrow{B1}+\overrightarrow{B2}\) có phương và chiều như hình vẽ, và có độ lớn:
\(B=B1\cos\alpha+B2\cos\alpha=2B1\cos\alpha=2B1.\frac{AH}{AM}=4.10^{-6}T\)
hình vẽ:
x x a a H I1 I2 M B B1 B2
Cảm ứng từ do dây I1 gây ra tại M là:
B1= 2.10-7 . \(\dfrac{100}{0,1}\) = 2.10-4 (T)
Cảm ứng từ do dây I2 gây ra tại M là:
B2 = 2.10-7 . \(\dfrac{100}{0,3}\) \(\simeq\) 6,67 . 10-5 (T)
Cảm ứng từ tổng hợp tại M là: \(\overrightarrow{B}=\overrightarrow{B_1}+\overrightarrow{B_2}\)
Vì 2 dòng điện cùng chiều nên cảm ứng từ ngược chiều:
B = B1 - B2 \(\simeq\) 1,33.10-4 (T)
Tỉ số \(\frac{U}{I}\) ở mỗi vật dẫn là khác nhau vì điện trở của mỗi loại vật dẫn khác nhau
R = \(\frac{U}{I}\)