Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A.
Ta có F ⇀ = q E ⇀
Mà q < 0 ® F có phương thẳng đứng, chiều từ dưới lên trên.
![]()

Ta có: \(\overrightarrow E = \frac{{\overrightarrow F }}{q}\)
Từ công thức ta thấy vectơ cường độ điện trường \(\overrightarrow E \) có phương trùng với phương của lực điện tác dụng lên điện tích
Với q > 0 thì \(\overrightarrow E \),\(\overrightarrow F \) cùng chiều với nhau
Với q < 0 thì \(\overrightarrow E \),\(\overrightarrow F \)ngược chiều với nhau
Nếu q = 1 thì E = F

Đoạn thẳng 1cm biểu diễn cho độ lớn của cường độ điện trường \(E = \frac{{{{10}^{ - 10}}}}{{6\pi {\varepsilon _0}}} = 0,6\)V/m.
Cường độ điện trường tại điểm cách Q một khoảng 2 cm:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{\left| {{{6.10}^{ - 14}}} \right|}}{{4\pi 8,{{85.10}^{ - 12}}.0,{{02}^2}}} = 1,34\)V/m
Vectơ cường độ điện trường:
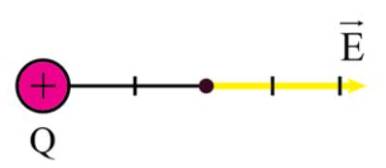
Cường độ điện trường tại điểm cách Q một khoảng 3 cm:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{\left| {{{6.10}^{ - 14}}} \right|}}{{4\pi 8,{{85.10}^{ - 12}}.0,{{03}^2}}} = 0,6\)V/m
Vectơ cường độ điện trường:
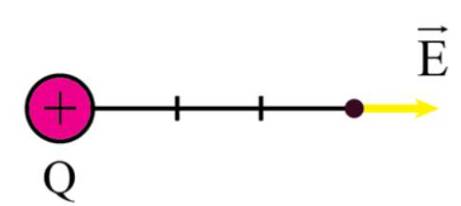

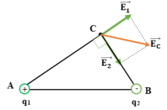
Điện trường do hai điện tích q1 và q2 gây ra tại C được biểu diễn như hình vẽ.
Ta có:
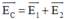
Trong đó:
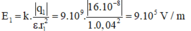
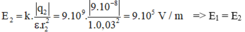
Vì AB = 5cm; AC = 4cm và BC = 3cm
⇒ ΔABC vuông tại C ⇒ 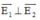
Suy ra 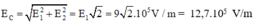
Và EC hợp với cạnh CB một góc 45o.
Đáp số: 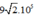 V/m
V/m

Đáp án C
Tại một điểm M trên đường sức điện trường, vectơ cường độ điện trường có phương trùng với tiếp tuyến với đường sức tại M.
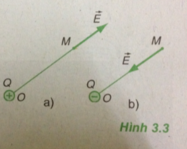



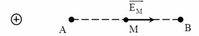
Giả sử tại M điện tích thử q > 0
• Ở trường hợp a): Q và q tích điên cùng dấu nên chúng đẩy nhau. Lực Cu-lông tác dụng nên điện tích q có chiều hướng ra xa Q. Do q > 0 nên E tại M cùng chiều với F nên cũng hướng ra xa Q ( > 0).
• Ở trường hợp b): Q và q tích điện trái dấu nên chúng hút nhau. Lực Cu-lông tác dụng nên q (tại M) hướng về phía Q. Do đó Q > 0 nên E tại M cùng chiều với F nên cũng hướng về phía Q (< 0).