Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phương của cường độ điện trường này trùng với đường nối của điện tích với điểm đang xét.
Chiều của cường độ điện trường hướng ra xa điện tích (do Q là điện tích dương).
Độ lớn của cường độ điện trường do điện tích điểm Q gây ra tại một điểm cách nó một khoảng 1 cm là:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{{{3.10}^{ - 9}}}}{{2\pi {\varepsilon _0}}}\)(V/m)
Độ lớn của cường độ điện trường do điện tích điểm Q gây ra tại một điểm cách nó một khoảng 2 cm là
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{{{15.10}^{ - 10}}}}{{4\pi {\varepsilon _0}}}\) (V/m)
Độ lớn của cường độ điện trường do điện tích điểm Q gây ra tại một điểm cách nó một khoảng 3 cm là
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{{{5.10}^{ - 10}}}}{{3\pi {\varepsilon _0}}}\) (V/m)
b) Càng gần điện tích thì cường độ điện trường càng mạnh, càng xa điện tích thì cường độ điện trường càng yếu. Phù hợp với công thức thể hiện mối quan hệ giữa cường độ điện trường và khoảng cách từ điện tích đến điểm xét: độ lớn cường độ điện trường tỉ lệ nghịch với bình phương khoảng cách từ điện tích đến điểm xét.
c) Cường độ điện trường do một điện tích điểm dương gây ra có:
- Phương: trùng với đường nối của điện tích với điểm đang xét.
- Chiều: hướng ra xa điện tích.
- Độ lớn: tỉ lệ nghịch với bình phương khoảng cách từ điện tích điểm đó đến điểm xét.

Chọn đáp án B
Công của lực điện trường trên đường gấp khúc ABC là
A A B C = A A B + A B C A A B = q . E . d 1 = q . E . A B . cos 30 ° = 0 , 692 . 10 - 6 J
A B C = q . E . d 2 = q . E . B C . cos 120 ° = - 0 , 8 . 10 - 6 J
→ A A B C = 0 , 692 . 10 - 6 - 0 , 8 . 10 - 6 = - 0 , 108 . 10 - 6 J

+ - A B C q1 q2 E1 E2 E
Nhận xét: Do \(AB^2=AC^2+BC^2\) nên tam giác ABC vuông tại C.
Điện trường tổng hợp tại C là: \(\vec{E}=\vec{E_1}+\vec{E_2}\)
Suy ra độ lớn: \(E=\sqrt{E_1^2+E_2^2}\) (*) (do \(\vec{E_1}\) vuông góc với \(\vec{E_2}\) )
\(E_1=9.10^9.\dfrac{16.10^{-8}}{0,04^2}=9.10^5(V/m)\)
\(E_1=9.10^9.\dfrac{9.10^{-8}}{0,03^2}=9.10^5(V/m)\)
Thay vào (*) ta được \(E=9\sqrt2.10^5(V/m)\)

A A B C = A A B + A B C
A A B = qE d 1 với q = +4. 10 - 8 C; E = 100V/m và d 1 = ABcos30 ° = 0,173m
A A B = 0,692. 10 - 6 J
A B C = qE d 2 với d 2 = BCcos120 ° = -0,2m; A B C = -0,8. 10 - 6 J
Vậy A A B C = - 0,108. 10 - 6 J.

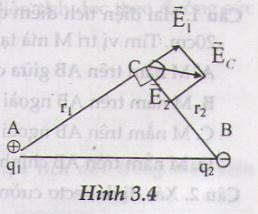
13. Hai điện tích điểm A và B cách nhau 5cm trong chân không có hai điện tích q1 = +16.10-8 C và q2 = - 9.10-8 C. Tính cường độ điện trường tổng hợp và vẽ vectơ cường độ điện trường tại điểm C nằm cách A một khoảng 4cm và cách B một khoảng 3cm.
Hướng dẫn giải.
Đặt AC = r1 và BC = r2 . Gọi −→E1E1→ và −→E2E2→ lần lượt là cường độ điện trường do q1 và q2 gây ra ở C (Hình 3.4).
E1=k.q1εr21E1=k.q1εr12= 9.105 V/m (Hướng theo phương AC).
E1=k.q2εr22E1=k.q2εr22 = 9.105 V/m (Hướng theo phương CB).
Vì tam giác ABC là tam giác vuông nên hai vectơ −→E1E1→ và −→E2E2→ vuông góc với nhau.
Gọi −→ECEC→ là vectơ cường độ điện trường tổng hợp :
−→ECEC→ = −→E1E1→ + −→E2E2→ => EC=√2E1=12,7.105EC=2E1=12,7.105 V/m.
Vectơ −→ECEC→ làm với các phương AC và BC những góc 450 và có chiều như hình vẽ.

Đáp án: B
Công của lực điện trường trên đường gấp khúc ABC là
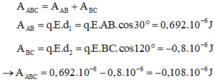

Đáp án B
Công của lực điện trường trên đường gấp khúc ABC là
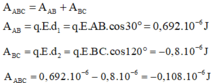
Đoạn thẳng 1cm biểu diễn cho độ lớn của cường độ điện trường \(E = \frac{{{{10}^{ - 10}}}}{{6\pi {\varepsilon _0}}} = 0,6\)V/m.
Cường độ điện trường tại điểm cách Q một khoảng 2 cm:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{\left| {{{6.10}^{ - 14}}} \right|}}{{4\pi 8,{{85.10}^{ - 12}}.0,{{02}^2}}} = 1,34\)V/m
Vectơ cường độ điện trường:
Cường độ điện trường tại điểm cách Q một khoảng 3 cm:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{\left| {{{6.10}^{ - 14}}} \right|}}{{4\pi 8,{{85.10}^{ - 12}}.0,{{03}^2}}} = 0,6\)V/m
Vectơ cường độ điện trường: