Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
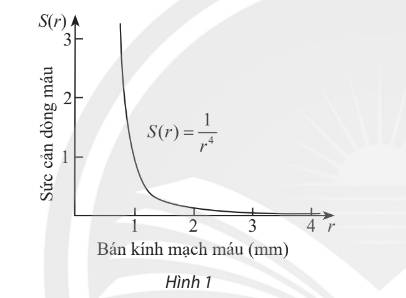
\(s'\left(r\right)=\left(\dfrac{1}{r^4}\right)'=-4\cdot r^{-5}=-\dfrac{4}{r^5}\)
Tốc độ thay đổi của S theo r khi \(r=0,8\) là:
\(S'\left(0,8\right)=-\dfrac{4}{0,8^5}\approx-12,21\)

a) t = 6
\( \Rightarrow B(6) = 80 + 7.\sin \frac{{\pi 6}}{{12}} = 80 + 7.\sin \frac{\pi }{2} = 87\)
b) t=10,5
\( \Rightarrow B(10,5) = 80 + 7.\sin \frac{{\pi 10,5}}{{12}} = 80 + 7.\sin \frac{{7\pi }}{8} = 82,67878\)
c) t=12
\( \Rightarrow B(12) = 80 + 7.\sin \frac{{\pi 12}}{{12}} = 80 + 7.\sin \pi = 80\)
d) t = 20
\(\begin{array}{l} \Rightarrow B(20) = 80 + 7.\sin \frac{{\pi 20}}{{12}} = 80 + 7.\sin \frac{{5\pi }}{3} = 80 + 7.\sin \left( {\pi + \frac{{2\pi }}{3}} \right) = 80 - 7.\sin \left( {\frac{{2\pi }}{3}} \right) = 80 - 7.\sin \left( {\pi - \frac{\pi }{3}} \right)\\ = 80 - 7.\sin \left( {\frac{\pi }{3}} \right) = \frac{{160 - 7\sqrt 3 }}{2}\end{array}\)

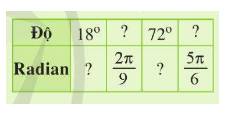
Ta có bảng chuyển đổi số đo độ và số đo radian của một số góc sau:
Độ | \({18^ \circ }\) | \(\frac{{2\pi }}{9}.\frac{{180}}{\pi } = {40^ \circ }\) | \({72^ \circ }\) | \(\frac{{5\pi }}{6}.\frac{{180}}{\pi } = {150^ \circ }\) |
Radian | \(18.\frac{\pi }{{180}} = \frac{\pi }{{10}}\) | \(\frac{{2\pi }}{9}\) | \(72.\frac{\pi }{{180}} = \frac{{2\pi }}{5}\) | \(\frac{{5\pi }}{6}\) |

a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
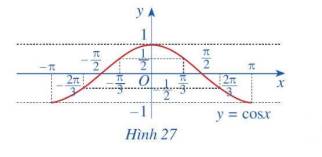
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
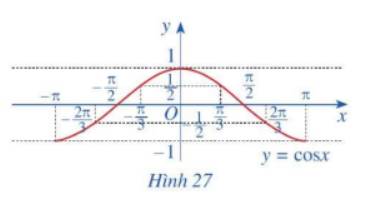
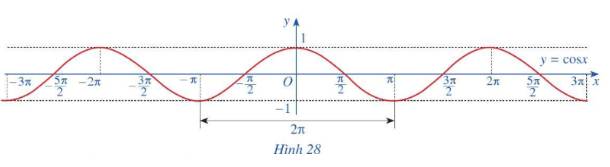
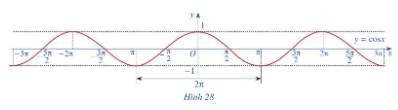
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

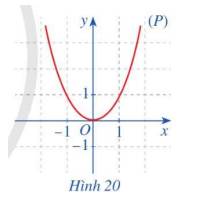
a)
Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2},f\left( x \right) = {x^2} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)
Trục đối xứng của (P) là đường thẳng y = 0
b)
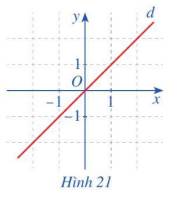
Ta có: \(g\left( { - x} \right) = - g\left( x \right)\)
Gốc tọa độ O là tâm đối xứng của đường thẳng d

a: Chu kì của hàm là: 2pi/160pi=1/80
b: Thời gian giữa hai lần tim đập là T=1/80
Số nhịp tim mỗi phút là 1/T=80(nhịp)
c: -1<=sin(160pi*t)<=1
=>-25<=25*sin(160*pi*t)<=25
=>90<=P(t)<=140
=>Chỉ số huyết áp là 140/90
=>Cao hơn người bình thường

a) Chu kỳ của hàm số \(p\left( t \right)\) là \(T = \frac{{2\pi }}{{160\pi }} = \frac{1}{{80}}\)
b) Thời gian giữa hai lần tim đập là \(T = \frac{1}{{80}}\) (phút)
Số nhịp tim mỗi phút là: \(\frac{1}{{\frac{1}{{80}}}} = 80\) (nhịp)
c) Ta có: \( - 1 \le sin\;\left( {160\pi t} \right)\; \le 1,\;\;\forall t \in R\)
\( \Leftrightarrow - 25 \le 25sin\;\left( {160\pi t} \right)\; \le 25,\;\forall t \in R\;\)
\( \Leftrightarrow 115 - 25 \le 115 + 25sin\;\left( {160\pi t} \right)\; \le 115 + 25,\;\forall t \in R\)
\( \Leftrightarrow 90 \le p\left( t \right) \le 140,\;\forall t \in R\)
Do đó, chỉ số huyết áp của người này là 140/90 và chỉ số huyết áp của người này cao hơn mức bình thường.



.png)
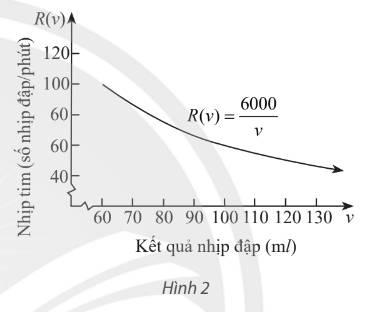
Ta có: \(R'\left(v\right)=6000\cdot\left(-\dfrac{1}{v^2}\right)=\dfrac{-6000}{v^2}\)
Tốc độ thay đổi của nhịp tim khi lượng máu tim đẩy đi ở một nhịp (v 80) là: \(R'\left(80\right)=-\dfrac{6000}{80^2}=-0,9375\)