Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (km/h) là vận tốc của máy bay cánh quạt. Điều kiện: x > 0
Ta có vận tốc của máy bay phản lực là x + 300 (km/h)
Thời gian máy bay cánh quạt bay là 600/x (giờ)
Thời gian máy bay phản lực bay là 600/(x + 300) (giờ)
Máy bay phản lực bay sau 10 phút và đến trước 10 phút nên thời gian máy bay phản lực bay ít hơn máy bay cánh quạt là:
10 phút + 10 phút = 20 phút = 1/3 (giờ)
Theo đề bài, ta có phương trình:
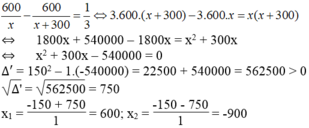
Giá trị x = -900 không thỏa mãn điều kiện bài toán.
Vậy vận tốc của máy bay cánh quạt là 600 km/h.
vận tốc của máy bay phản lực là 600 + 300 = 900 km/h

1.
Theo đề bài, suy ra thời gian đi từ Hà Nội đến Đà Nẵng của máy bay phản lực ít hơn máy bay trực thăng $20$ phút, tức $\frac{1}{3}$ h.
Gọi vận tốc của máy bay phản lực là $a$ km/h thì vận tốc máy bay trực thăng là $a-300$ (km/h). ĐK: $a>300$
Theo bài ra ta có:
$\frac{600}{a-300}-\frac{600}{a}=\frac{1}{3}$
$\Leftrightarrow a(a-300)-540000=0$
$\Leftrightarrow (a-900)(a+600)=0$
$\Rightarrow a=900$ (km/h) (vận tốc mb phản lực)
Vận tốc mb trực thăng: $a-300=600$ (km/h)
2.
Gọi đỉnh núi là $A$. Hai điểm cách nhau 1 m lần lượt là $B,C$.
Từ $A$ kẻ $AH\perp BC$. $AH$ chính là chiều cao của ngọn núi.
Ta có:
$\frac{AH}{BH}=\tan B=\tan 40^0$
$\frac{AH}{CH}=\tan C=\tan 32^0$
$\Rightarrow AH=BH\tan 40^0=CH\tan 32^0=\frac{BH+CH}{\frac{1}{\tan 40}+\frac{1}{\tan 32}}=\frac{1}{\frac{1}{\tan 40}+\frac{1}{\tan 32}}=0,36$ (km)

Gọi x,y ( km/h ) lần lượt là vận tốc của máy bay trực thăng và máy bay phản phản lực ( ĐK: x,y > 0 )
Thời gian máy bay trực thăng bay từ Đà Năng ra Hà Nội là : \(\dfrac{600}{x}\) ( giờ )
Thời gian máy bay phản lực bay từ Hà Nội ra Đà Nẵng là : \(\dfrac{600}{y} \) ( giờ )
Vì vận tốc máy bay phản lực lớn hơn vận tốc trực thăng là 300km/h nên ta có phương trình : y - x = 300 ( 1 )
Vì sau khi trực thăng xuất phát 10p thì máy bay phản lực xuất phát và đến sớm hơn trực thăng 10p nên ta có phương trình : \(\dfrac{600}{x}\) = \(\dfrac{600}{y}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{6}\) ⇔ \(\dfrac{600}{x}\) = \(\dfrac{600}{y}\) + \(\dfrac{2}{3}\) ( 2 )
Từ (1) và (2) => \(\begin{cases} y - x = 300 \\ \dfrac{600}{x}=\dfrac{600}{y} + \dfrac{2}{3} \end{cases} \)⇔ \(\begin{cases} y = 300 + x \\ \dfrac{600}{x} = \dfrac{600}{x + 300} +\dfrac{2}{3} \end{cases} \) ⇔\(\begin{cases} y=300+x\\ 600x + 180000 = 600x + \dfrac{2}{3}.x^2+200x \end{cases} \)⇔ \(\begin{cases} y=300+x\\ \dfrac{2}{3}x^2 + 200x - 180000 (*) \end{cases} \)
Giải phương trình (*) ta dc \(\left[\begin{array}{} x = 390,83( nhận)\\ x= -690,83(loại) \end{array} \right.\)=> \(\begin{cases} x = 390,83\\ y = 690,83 \end{cases} \)
Vậy...

Quãng đường xiên mà máy bay bay được :
\(600.\left(1,5:60\right)=15\left(km\right)\)
Sau 15 phút, máy bay bay được độ cao :
\(x=\sin30.15=7,5\left(km\right)\)
\(t=1,5\left(phút\right)=0,025\left(giờ\right)\)
Quãng đường bay sau \(0,025\left(giờ\right)\)
\(s=v.t=600.0,025=15\left(km\right)\)
Độ cao theo phương thẳng đứng là :
\(sin30^o=\dfrac{h}{s}\Rightarrow h=s.sin30^o=15.\dfrac{1}{2}=7,5\left(km\right)\)
