Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Theo đề bài, suy ra thời gian đi từ Hà Nội đến Đà Nẵng của máy bay phản lực ít hơn máy bay trực thăng $20$ phút, tức $\frac{1}{3}$ h.
Gọi vận tốc của máy bay phản lực là $a$ km/h thì vận tốc máy bay trực thăng là $a-300$ (km/h). ĐK: $a>300$
Theo bài ra ta có:
$\frac{600}{a-300}-\frac{600}{a}=\frac{1}{3}$
$\Leftrightarrow a(a-300)-540000=0$
$\Leftrightarrow (a-900)(a+600)=0$
$\Rightarrow a=900$ (km/h) (vận tốc mb phản lực)
Vận tốc mb trực thăng: $a-300=600$ (km/h)
2.
Gọi đỉnh núi là $A$. Hai điểm cách nhau 1 m lần lượt là $B,C$.
Từ $A$ kẻ $AH\perp BC$. $AH$ chính là chiều cao của ngọn núi.
Ta có:
$\frac{AH}{BH}=\tan B=\tan 40^0$
$\frac{AH}{CH}=\tan C=\tan 32^0$
$\Rightarrow AH=BH\tan 40^0=CH\tan 32^0=\frac{BH+CH}{\frac{1}{\tan 40}+\frac{1}{\tan 32}}=\frac{1}{\frac{1}{\tan 40}+\frac{1}{\tan 32}}=0,36$ (km)

Gọi x,y ( km/h ) lần lượt là vận tốc của máy bay trực thăng và máy bay phản phản lực ( ĐK: x,y > 0 )
Thời gian máy bay trực thăng bay từ Đà Năng ra Hà Nội là : \(\dfrac{600}{x}\) ( giờ )
Thời gian máy bay phản lực bay từ Hà Nội ra Đà Nẵng là : \(\dfrac{600}{y} \) ( giờ )
Vì vận tốc máy bay phản lực lớn hơn vận tốc trực thăng là 300km/h nên ta có phương trình : y - x = 300 ( 1 )
Vì sau khi trực thăng xuất phát 10p thì máy bay phản lực xuất phát và đến sớm hơn trực thăng 10p nên ta có phương trình : \(\dfrac{600}{x}\) = \(\dfrac{600}{y}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{6}\) ⇔ \(\dfrac{600}{x}\) = \(\dfrac{600}{y}\) + \(\dfrac{2}{3}\) ( 2 )
Từ (1) và (2) => \(\begin{cases} y - x = 300 \\ \dfrac{600}{x}=\dfrac{600}{y} + \dfrac{2}{3} \end{cases} \)⇔ \(\begin{cases} y = 300 + x \\ \dfrac{600}{x} = \dfrac{600}{x + 300} +\dfrac{2}{3} \end{cases} \) ⇔\(\begin{cases} y=300+x\\ 600x + 180000 = 600x + \dfrac{2}{3}.x^2+200x \end{cases} \)⇔ \(\begin{cases} y=300+x\\ \dfrac{2}{3}x^2 + 200x - 180000 (*) \end{cases} \)
Giải phương trình (*) ta dc \(\left[\begin{array}{} x = 390,83( nhận)\\ x= -690,83(loại) \end{array} \right.\)=> \(\begin{cases} x = 390,83\\ y = 690,83 \end{cases} \)
Vậy...

Gọi x (km/h) là vận tốc của máy bay cánh quạt. Điều kiện: x > 0
Ta có vận tốc của máy bay phản lực là x + 300 (km/h)
Thời gian máy bay cánh quạt bay là 600/x (giờ)
Thời gian máy bay phản lực bay là 600/(x + 300) (giờ)
Máy bay phản lực bay sau 10 phút và đến trước 10 phút nên thời gian máy bay phản lực bay ít hơn máy bay cánh quạt là:
10 phút + 10 phút = 20 phút = 1/3 (giờ)
Theo đề bài, ta có phương trình:
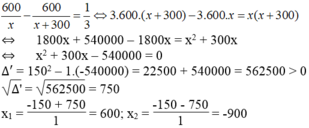
Giá trị x = -900 không thỏa mãn điều kiện bài toán.
Vậy vận tốc của máy bay cánh quạt là 600 km/h.
vận tốc của máy bay phản lực là 600 + 300 = 900 km/h

Gọi C là vị trí của máy bay
Gọi CH là độ cao của máy bay so với mặt đất
=>CH\(\perp\)AB tại H
Ta có hình vẽ sau:
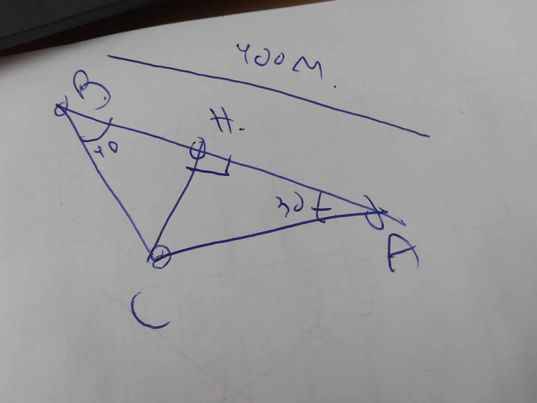
Xét ΔCBA có \(\widehat{CBA}+\widehat{CAB}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+40^0=180^0\)
=>\(\widehat{ACB}=110^0\)
Xét ΔABC có \(\dfrac{BA}{sinACB}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
=>\(\dfrac{400}{sin110}=\dfrac{AC}{sin40}=\dfrac{BC}{sin30}\)
=>\(AC\simeq273,62\left(m\right);BC\simeq212,84\left(m\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)
\(=\dfrac{1}{2}\cdot273,62\cdot212,84\cdot sin110\simeq27362,57\left(m^2\right)\)
Xét ΔACB có CH là đường cao
nên \(\dfrac{1}{2}\cdot CH\cdot AB=S_{ABC}\)
=>\(CH\cdot\dfrac{400}{2}=27362,57\)
=>\(CH\simeq136,81\left(m\right)\)


Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
![]()
Xét tam giác ADC vuông tại C có:
![]()
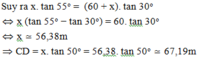
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C

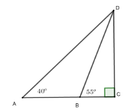
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Đáp án cần chọn là: A
