Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

SGK ... Tam giác cân không có tâm đối xứng đâu... Trục đối xứng của tam giác cân là ... Khó nói quá . VD nha : tam giác ABC cân tại A TH1 : kẻ AH vuông góc với BC => AH là trục đối xứng ( CM được tam giác ABH = ACH => ĐPCM) (1)
TH2 : Kẻ trung tuyến AI vì tam giác ABC cân tại A nên => AI vừa là trung tuyến vừa là đường cao => Tương tự (1)
Nhớ được các trường hợp đặc biệt của các đường trung tuyến, phân giác, đường cao ..v..v... trong tam giác cân thì cứ biện luận thôi, không cần phải giải thích nhiều vì ta công nhận điều đó là đúng ...

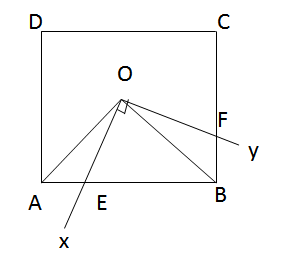
Nối OA, OB.
Xét \(\Delta\)AOE và \(\Delta\)BOF có:
+ \(\widehat{AOE}=\widehat{BOF}\) (cùng phụ với \(\widehat{BOE}\))
+ OA = OB (O là tâm đối xứng)
+ \(\widehat{OAE}=\widehat{OBE}=45^o\)
=> ∆AOE = ∆BOF (g - c - g)
Do đó: \(S_{OEBF}=S_{OEB}+S_{OBF}=S_{OEB}+S_{OAE}=S_{OAE}+S_{OEB}=S_{OAB}\)
Vậy \(S_{OEBF}=\dfrac{1}{4}S_{ABCD}\)
Nối OA, OB.
Xét ΔAOE và ΔBOF có:
+) \(\widehat{AOE}=\widehat{BOF}\) ( cùng phụ với BOE )
+) OA = OB ( O là tâm đối xứng )
+) \(\widehat{OAE}=\widehat{OBF}=45^0\)
⇒ ΔAOE = ΔBOF.
⇒ \(S_{OEBF}=S_{OEB}+S_{OBF}=S_{OEB}+S_{OAE}=S_{OAE}+S_{OAB}\)
⇒ \(S_{OEBF}=\frac{1}{4}S_{ABCD}.\)

Bài toán này rất hay, cô sẽ giải thích cho em nhé :)
Xét tam giác FAH và tam giác FAI có:
AI = AH ( Vì cùng bằng AE).
AF chung.
Ta cần chứng minh góc FAI = góc HAF.
Gọi giao điểm AB với IE là M, của AC với EH là N.
Khi đó ta có góc FAI = góc IAM + MAE + EAF = góc EAF + 2 góc FAN. (1)
góc HAF = góc FAN + NAH, mà góc NAH = góc EAF + góc FAN nên góc HAF = góc EAF + 2 góc FAN. (2)
Từ (1), (2) suy ra góc FAI = góc HAF.
Vậy tam giác FAI bằng tam goác FAH (c-g-c).
và đây là hình,nó có vẻ hơi xấu và sai 1 số chỗ nhỏ bạn thông cảm
I A H C K F E B

Ta có :
\(S_{ABC}=\frac{1}{2}.AH.BC=\frac{10.6}{2}=30\)( đvdt )
\(S_{ABC}=\frac{1}{2}\cdot AH\cdot BC=\frac{1}{2}\cdot6\cdot10=30\)