K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
21 tháng 7 2021
Để A là số nguyên thì
\(2x+12\ge x^2+x\)
\(\Leftrightarrow-3\le x\le4\)
Kết hợp với điều kiện đề bài được
\(1\le x\le4\)
Thế lần lược \(x=1;2;3;4\)cái nào làm cho A nguyên thì chọn
25 tháng 6 2021
7)Đk \(x\le2\)
Pt \(\Leftrightarrow x^2-x+8=4-2x\)
\(\Leftrightarrow x^2+x+4=0\)
\(\Delta=-15< 0\) => vô nghiệm
Vậy pt vô nghiệm
10) \(\sqrt{9x+9}-4\sqrt{\dfrac{x+1}{4}}=5\) (đk: \(x\ge-1\)
\(\Leftrightarrow\sqrt{\left(x+1\right).9}-\dfrac{4\sqrt{x+1}}{\sqrt{4}}=5\)
\(\Leftrightarrow3\sqrt{x+1}-2\sqrt{x+1}=5\)
\(\Leftrightarrow\sqrt{x+1}=5\) \(\Leftrightarrow x=24\) (tm)
Vậy \(S=\left\{24\right\}\)
M
2
25 tháng 6 2021
19) Ta có: \(\sqrt[3]{x^3+9x^2}=x+3\)
\(\Leftrightarrow x^3+9x^2=\left(x+3\right)^3\)
\(\Leftrightarrow x^3+9x^2=x^3+9x^2+27x+27\)
\(\Leftrightarrow27x+27=0\)
\(\Leftrightarrow27x=-27\)
hay x=-1
Vậy: S={-1}
6) Ta có: \(\sqrt{9x^2-6x+1}-x=4\)
\(\Leftrightarrow\sqrt{\left(3x-1\right)^2}=x+4\)
\(\Leftrightarrow\left|3x-1\right|=x+4\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=x+4\left(x\ge\dfrac{1}{3}\right)\\1-3x=x+4\left(x< \dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-x=4+1\\-3x-x=4-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\-4x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(nhận\right)\\x=\dfrac{-3}{4}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{5}{2};\dfrac{-3}{4}\right\}\)
25 tháng 6 2021
8)
ĐKXĐ: \(x>2\)
Ta có: \(\sqrt{x^2+2x+4}=x-2\)
\(\Leftrightarrow x^2+2x+4=\left(x-2\right)^2\)
\(\Leftrightarrow x^2+2x+4-x^2+4x-4=0\)
\(\Leftrightarrow6x=0\)
hay x=0(loại)
Vậy: \(S=\varnothing\)
9) Ta có: \(\sqrt{x^2-6x+9}=5\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=5\)
\(\Leftrightarrow\left|x-3\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=5\\x-3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
Vậy: S={8;-2}
E
1
8 tháng 8 2021
ta có sinB=\(\dfrac{AH}{AB}\)\(\Rightarrow\)AH=AB.sinB=3,6.sin62=3,18
BH=\(\sqrt{AB^2-AH^2}\)(pytago)=\(\sqrt{3,6^2-3,18^2}\)=1,69
\(_{\widehat{C}}\)=90-\(\widehat{B}\)=90-62=28\(^0\)
sinC=\(\dfrac{AB}{BC}\)\(\Rightarrow\)BC=\(\dfrac{AB}{sinC}\)=\(\dfrac{3,6}{sin28}\)=7,67
mà:CH=BC-BH=7,67-1,69=5,98
AC=\(\sqrt{BC^2-AB^2}\)(pytago)=\(\sqrt{7,67^2-3,6^2}\)=6.77
TD
0
AH
Akai Haruma
Giáo viên
18 tháng 7 2023
Bạn nên ghi đầy đủ đề cũng như điều kiện của $x$ để được hỗ trợ tốt hơn.
giải giúp mấy bài này đi mấy bạn
28 tháng 6 2021
â)ĐK;`x-2>=0`
`<=>x>=2`
c)ĐK:`2017/x>=0(x ne 0)`
Mà `2017>0`
`<=>x>0`
e)ĐK:`x^2+2017>=0`
`<=>x^2>=-2017AAx in RR`
b)ĐK:`2-3x>=0`
`<=>3x<=2`
`<=>x<=2/3`
d)ĐK:`(-2017)/(5-x)>=0(x ne 5)`
`<=>2017/(x-5)>=0`
Mà `2017>0`
`<=>x-5>0<=>x>5`
f)ĐK:`1-x^2>=0`
`<=>x^2<=1`
`<=>-1<=x<=1`
ZS
3
31 tháng 8 2021
m2 -8m -16 =0
m2 -2.4m -4\(^2\) =0
(m - 4)\(^2\) = 0
=> m -4 = 0
=> m = 4
HT
31 tháng 8 2021
m2 - 8m - 16 = 0 <=> m2 - 8m + 16 - 32 = 0
<=> ( m - 4 )2 - ( 4√2 )2 = 0 <=> ( m - 4 - 4√2 )( m - 4 + 4√2 ) = 0
<=> m = 4 ± 4√2
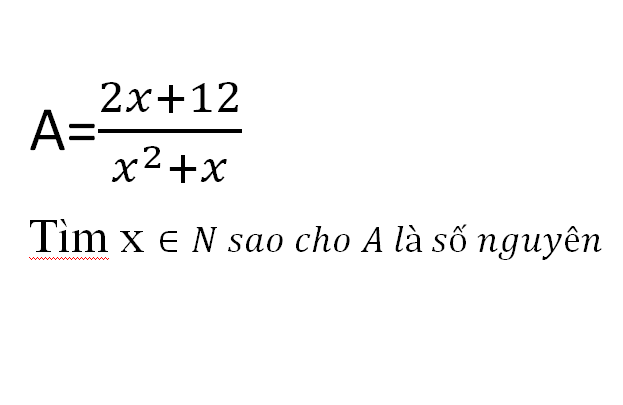
Bài 1: Để căn thức có nghĩa thì \(8x+2\ge0\Leftrightarrow x\ge\frac{-1}{4}\)
Bài 2: a) \(\sqrt{3}-\frac{1}{3}.\sqrt{27}+2\sqrt{507}=\sqrt{3}-\frac{1}{3}.3\sqrt{3}+2\sqrt{507}=2\sqrt{507}\)
b) \(\frac{1}{3-\sqrt{2}}=\frac{3+\sqrt{2}}{\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)}=\frac{3+\sqrt{2}}{7}\)
c) \(5\sqrt{2}-\sqrt{\left(5\sqrt{2}-1\right)^2}=5\sqrt{2}-5\sqrt{2}+1=1\)
Bài 2: \(3\sqrt{4x+20}-4\sqrt{5+x}=6\)
\(\Leftrightarrow6\sqrt{x+5}-4\sqrt{x+5}=6\)
\(\Leftrightarrow2\sqrt{x+5}=6\Leftrightarrow\sqrt{x+5}=3\)
\(\Leftrightarrow x+5=9\Leftrightarrow x=4\)
Vậy x = 4